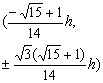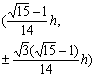§2 多重积分、曲线积分与曲面积分
一、多重积分
1. 二重积分
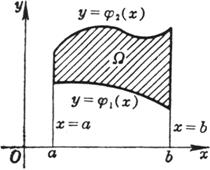
连续函数f(x,y)在有限可求积的平面区域Ω内的二重积分
![]()
式中![]() ,
,![]() ,
,![]() 是对Ω中的所有
是对Ω中的所有![]() 的下标i,j求和.
的下标i,j求和.
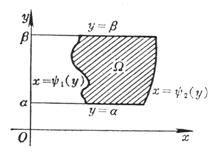
[特定区域内二重积分的计算公式]
|
积分区域Ω |
|
|
|
设
|
[二重积分的变量替换(雅可比式)] 若连续可微分的函数
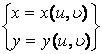
把平面Oxy上的有界闭区域Ω单值映射到平面![]() 上的闭区域Ω',其雅可比式为
上的闭区域Ω',其雅可比式为
![]()
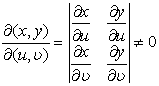
则
![]()
例 若
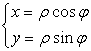
则
![]()
![]()
所以
![]()
2. 三重积分
[直角坐标下的三重积分] 假设有界区域V由下列不等式
a≤x≤b, ![]() ≤y≤
≤y≤![]() ,
, ![]() ≤z≤
≤z≤![]()
确定,其中![]() ,
,![]() ,
,![]() ,
,![]() 都是连续函数,且函数f(x,y,z)在V上是连续的,则函数f(x,y,z)在有界区域V上的三重积分
都是连续函数,且函数f(x,y,z)在V上是连续的,则函数f(x,y,z)在有界区域V上的三重积分
![]()
有时采用下面公式计算:
![]()
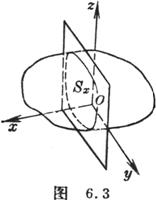
式中![]() 是用平行于Oyz的平面截区域V所得的截断面(图6.3).
是用平行于Oyz的平面截区域V所得的截断面(图6.3).
例 设V表示在第一卦限中由曲面![]() 和坐标平面所围成的封闭区域,则当一切常数都是正的时候,有
和坐标平面所围成的封闭区域,则当一切常数都是正的时候,有
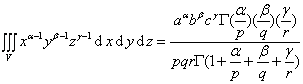
这种类型的积分称为狄利克莱积分,它在计算重积分时经常用到.
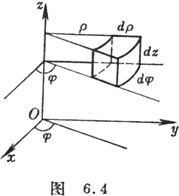
[圆柱坐标下的三重积分] (图6.4)
![]()
(一般地,0≤![]() ≤2π)
≤2π)
式中V为直角坐标中的有界区域,V'是区域V在圆柱坐标系中的表达式.
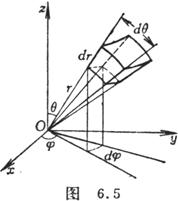
[球面坐标下的三重积分] (图6.5)
![]()
(一般地,0≤![]() ≤2π,0≤θ≤π)
≤2π,0≤θ≤π)
式中V'是区域V在球面坐标系中的表达式.
[三重积分的变量替换(雅可比式)] 若连续可微函数
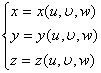
把Oxyz空间的有界三维闭区域双方单值地映射到O'u![]() w空间的闭区域V',并且当(u,
w空间的闭区域V',并且当(u, ![]() ,w)∈V'时其雅可比式
,w)∈V'时其雅可比式
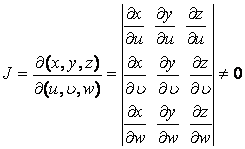
则
![]()
3. 多重积分
[直接计算多重积分] 若函数f(![]() )在由下列不等式所确定的有界闭区域Ω内是连续的:
)在由下列不等式所确定的有界闭区域Ω内是连续的:
a≤![]() ≤b
≤b
![]() (
(![]() )≤
)≤![]() ≤
≤![]() (
(![]() )
)
………………………
![]() (
(![]() )≤
)≤![]() ≤
≤![]() (
(![]() )
)
式中a,b为常数,![]() (
(![]() ),
),![]() (
(![]() ),…,
),…,![]() (
(![]() ),
),![]() (
(![]() )为连续函数,则对应的多重积分可按下面公式计算:
)为连续函数,则对应的多重积分可按下面公式计算:
![]()
[多重积分的变量替换(雅可比式)] 若连续可微函数
![]() =
=![]() (
(![]() ), i=1,2,…,n
), i=1,2,…,n
把O![]() 空间内的有界闭区域Ω双方单值地映射成O'
空间内的有界闭区域Ω双方单值地映射成O'![]() 空间内的有界闭区域Ω',并且在闭区域Ω'内雅可比式
空间内的有界闭区域Ω',并且在闭区域Ω'内雅可比式
![]()
则
![]()
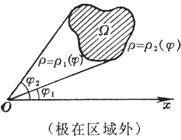
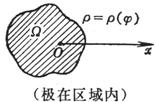
特别,根据公式
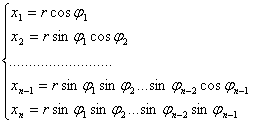
变换成极坐标(r,![]() )时,有:
)时,有:
![]()
二、曲线积分
|
|
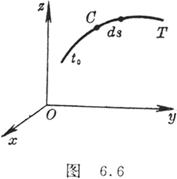
[对弧长的曲线积分] 若函数f(x,y,z)在光滑曲线C:
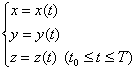
的各点上有定义并且连续(图6.6)则
![]()
式中ds为弧的微分,![]() 等.这个积分与曲线C的方向无关.
等.这个积分与曲线C的方向无关.
[对坐标的曲线积分] 若函数P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)在光滑曲线C:
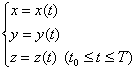
的各点上连续,这曲线的正方向为t增加的方向,则
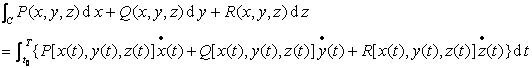
当曲线C的正向变更时,积分的符号改变.
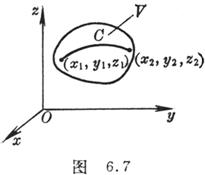
[全微分的情形] 若函数P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)在区域V中的任一条光滑曲线C上连续,并且
![]()
式中u=u(x,y,z)为区域V内的单值可微函数,则
![]()
式中(![]() )为积分曲线C的始点,(
)为积分曲线C的始点,(![]() )为积分曲线C的终点.这说明在假定的条件下,积分值与曲线C的形状无关,只与曲线的始点和终点有关(图6.7).
)为积分曲线C的终点.这说明在假定的条件下,积分值与曲线C的形状无关,只与曲线的始点和终点有关(图6.7).
在单连通区域V内有连续的一阶偏导数的函数P,Q,R能表成全微分
![]()
的充分必要条件是:在区域V内等式
![]()
成立.这时函数u可按下面公式求得:
![]()
式中(![]() )为区域V内的某一固定点.
)为区域V内的某一固定点.
|
|
[格林公式]
1°曲线积分与二重积分的关系.设C为逐段光滑的简单(无自交点)闭曲线,围成单连通的有界区域S,这围线的方向使区域S保持在左边,若函数P(x,y),Q(x,y)及它们的一阶偏导数在S+C上连续,则有格林公式 :
![]()
|
|
2° 曲线积分与积分线路的关系.若函数P,Q,![]() 在区域S上连续,且
在区域S上连续,且
![]()
则沿S内的任一光滑闭曲线的积分为零,即
![]()
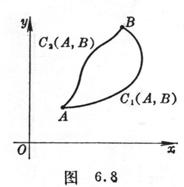
因而由S中的A到B的积分与线路无关(图6.8),即
![]()
三、曲面积分
[对曲面面积的曲面积分]
1° 若S为逐片光滑的双侧曲面*
z=z(x,y)
((x,y)![]() )
)
式中σ为曲面S在Oxy坐标面上的投影,z(x,y)为单值连续可微函数,函数f(x,y,z)在曲面S的各点上有定义并连续,则
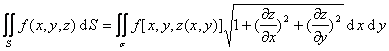
此积分与曲面S的方向(法线的方向)无关.
2° 若曲面S由连续可微函数
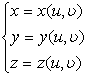 ((u,
((u,![]() )∈Ω)
)∈Ω)
给定,则
![]()
式中
![]()
![]()
![]()
![]()
* 曲面上某一点的法线方向的选定,唯一确定了曲面上所有其他点的法线方向,它们就是选定方向的
法线在曲面上连续移动(不经过曲面边缘)的指向,所以也就决定了曲面的一侧.如果改变原来选定
的法线方向,曲面上的所有其他点的法线方向都随着改变,曲面就从一侧移到另一侧.这种曲面称为
双侧曲面.
[对坐标的曲面积分] 若S为光滑的双侧曲面,![]() 为它的正面,即由法线方向n(cosα, cosβ,cosγ)所确定的一侧,P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)为在曲面S上有定义并且连续的函数,则
为它的正面,即由法线方向n(cosα, cosβ,cosγ)所确定的一侧,P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)为在曲面S上有定义并且连续的函数,则
![]()
若曲面S由连续可微函数
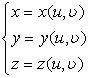 ((u,
((u,![]() )∈Ω)
)∈Ω)
给定,则
![]()
式中
![]()
[斯托克斯公式] 若C是包围逐片光滑有界双侧曲面S的逐段光滑简单闭曲线,P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)是在S+C上连续可微函数,则
![]()
[高斯公式] 若S为包含体积V的逐片光滑曲面P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)及其一阶偏导数在V+S上连续,则有高斯公式:
![]()
式中cosα,cosβ,cosγ为曲面S的法线正方向的方向余弦.
四、 重积分、曲线积分与曲面积分的近似计算
[二重积分的近似计算公式]
![]()
式中![]() 对于不同的积分区域Ω选取不同的常数,
对于不同的积分区域Ω选取不同的常数,![]() 是求积系数,R是余项.
是求积系数,R是余项.
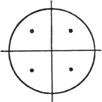
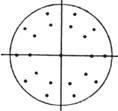
Ω为圆形C: ![]() ≤
≤![]() Ac=π
Ac=π![]()
|
n |
图示 |
|
|
R |
|
5 |
|
(0,0)
(±h,0)
(0,±h) |
|
|
|
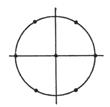
4 |
|
|
|
|
|
n |
图示 |
|
|
R |
|
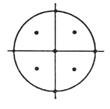
7 |
|
(0,0)
(±h,0)
|
|
|
|
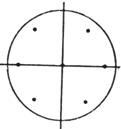
9 |
|
(0,0)
(±h,0)
(0, ±h)
|
|
|
|
7 |
|
(0,0)
(±
(± |
|
|
|
21 |
|
(0,0) (
(
k=1,2,…,10 |
|
|
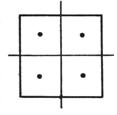
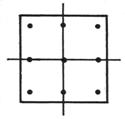
Ω为正方形S: |x|≤h,|y|≤h , ![]() =4
=4![]()
|
n |
图示 |
|
|
R |
|
9 |
|
(0,0)
(±h,±h)
(±h,0)
(0, ±h)
|
|
|
|
n |
图示 |
|
|
R |
|
4 |
|
|
|
|
|
9 |
|
(0,0)
|
|
|
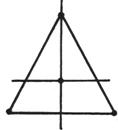
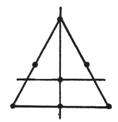
Ω为正三角形T: 外接圆半径为h,![]()
|
n |
图示 |
|
|
R |
|
4 |
|
(0,0)
(h,0)
|
|
|
|
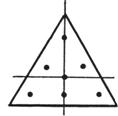
7 |
|
(0,0)
|
|
|
|
7 |
|
(0,0)
|
|
|
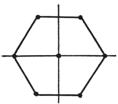
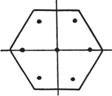
Ω为正六边形H: 外接半径为h,![]()
|
n |
图示 |
|
|
R |
|
7 |
|
(0,0)
(
|
|
|
|
7 |
|
(0,0)
|
|
|
[三重积分的近似计算公式]
![]()
式中![]() 对于不同的积分区域V选取不同的常数,
对于不同的积分区域V选取不同的常数,![]() 是求积系数,R是余项.
是求积系数,R是余项.
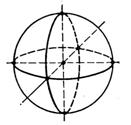
V为球体S: ![]() ≤
≤![]() .
. ![]() =
=![]() π
π![]()
|
n |
图示 |
|
|
R |
|
7 |
|
(0,0,0)
|
|
|
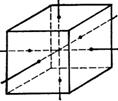
V为立方体C: |x|≤h,|y|≤h,|z|≤h. ![]() =8
=8![]()
|
n |
图示 |
|
|
R |
|
6 |
|
|
|
|
|
21 |
|
(0,0,0) 中心到6个面的距离的6个中点
6个面的中心
8个顶点 |
|
|
|
n |
图示 |
|
|
R |
|
42 |
|
6个面的中心
12个棱的中点
每个面的对角线上到每个面中心距离为 24点) |
|
|
Ω为四面体T.![]() 为四面体体积
为四面体体积
|
n |
图示 |
|
|
R |
|
8
11 |
|
4个顶点
4个面的重心
T的重心
4个顶点
6个棱的中点
|
|
|
[曲线积分的近似计算公式]
|
|
圆周![]() :
:![]() 上的曲线积分
上的曲线积分
![]()
[曲面积分的近似计算公式]
球面![]() :
:![]() 上的曲面积分
上的曲面积分
![]()
|
n |
图示 |
|
|
R |
|
6
|
|
|
|
|
|
n |
图示 |
|
|
R |
|
18 |
|
|
|
|
|
26 |
|
|
|
|