[相似变换] 如果有一非奇异矩阵X(即det X¹ 0)使得
B=![]() AX
AX
那末称矩阵A与矩阵B相似,也称A经相似变换化为B,记作A~ B.它具有下列性质:
1° A~ A,At ~ A.
2° 若A~ B,则B~ A.
3° 若A~ C,B~ C,则A~ B.
4° ![]() (A1+
A2+...+ Am)X=
(A1+
A2+...+ Am)X=![]() A1X+
A1X+![]() A2X+
...+
A2X+
...+![]() AmX
AmX
5° ![]()
6° ![]() AmX=(
AmX=(![]() AX)m
AX)m
7° 若![]() 为矩阵A的多项式,则
为矩阵A的多项式,则
![]()
![]() X=
X=![]()
8° 若A~ B,则
A与B的秩相同,即rank A=rank B.
A与B的行列式相同,即det A=det B.
A与B的迹(定义见本节,七)相同,即tr A=tr B.
A与B具有相同的特征多项式和特征值(本节,七).
[正交变换] 若Q为正交矩阵(即![]() =Qt
),则称
=Qt
),则称
Qt AQ
为矩阵A的正交变换,其性质与相似变换类似.特别还有性质:
对称矩阵A经正交变换后仍是对称矩阵.
[旋转变换] 取正交矩阵U为
![]()
![]()
Upq=(uij)=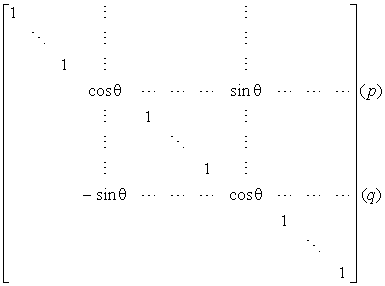
即
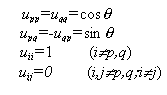
这时称
B=![]()
为A的旋转变换,q 称为旋转角,如果A是对称矩阵,那末B的元素bij与A的元素aij有
如下对应关系:
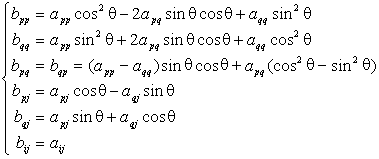
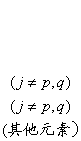
同时有性质:
![]() =
=![]()
![]()
![]()
若取旋转角
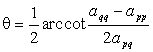
则旋转变换使
![]()