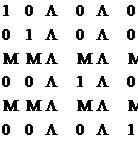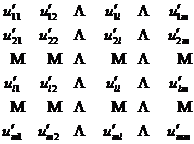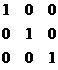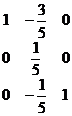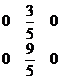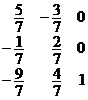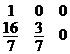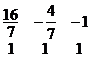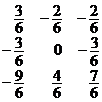除了将和第![]() 行的最大正数相对应的矢量引进基底以外,表3和表1一样处理.第
行的最大正数相对应的矢量引进基底以外,表3和表1一样处理.第![]() 行的元素也用通常的主元素消去法公式加以变换.一旦将一人工矢量从基底消去,就不再进入基底,所以没有必要去变换表中最后的
行的元素也用通常的主元素消去法公式加以变换.一旦将一人工矢量从基底消去,就不再进入基底,所以没有必要去变换表中最后的![]() 列.继续进行上述迭代直到所有人工矢量都从基底消去,或者第
列.继续进行上述迭代直到所有人工矢量都从基底消去,或者第![]() 行没有正的元素存在.
行没有正的元素存在.
如果原来的问题包含一些单位矢量,那末这些矢量可以和必要的人工矢量一起作为初始基底,这样可以减少迭代次数.
例1 极大化 ![]()
满足条件
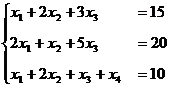
和
![]()
解 把上述问题改为极小化
![]() .
.
由于给定系统包含一单位矢量![]() ,因此只需要两个人工矢量
,因此只需要两个人工矢量![]() 和
和![]() ,与
,与![]() 一起作为初始基底.第一个解(表4)为
一起作为初始基底.第一个解(表4)为![]()
![]() ,相应的目标函数值等于
,相应的目标函数值等于![]() .
.![]() 的计算可由
的计算可由![]() 和矢量
和矢量![]() 的内积得到.例如
的内积得到.例如
![]()
因为(![]() )的极大元素为5,所以将矢量
)的极大元素为5,所以将矢量![]() 引进基底.相应的
引进基底.相应的![]() ,故人工矢量
,故人工矢量![]() 从基底消去,用主元素消去公式变换表4中第1步的所有元素,相应的目标函数值为
从基底消去,用主元素消去公式变换表4中第1步的所有元素,相应的目标函数值为![]() ,新解为
,新解为![]()
![]() ,.
,.![]() 引进基底,
引进基底,![]() 从基底消去.在第3步,由于所有的
从基底消去.在第3步,由于所有的![]() 而且
而且![]() ,得到原来问题的一个可行解
,得到原来问题的一个可行解
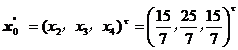
表 4
第1步
|
|
基底 |
|
|
-1 |
-2 |
-3 |
1 |
|
|
|
|
|
|
|
|
|
||||
|
2 3 |
|
1 |
15 20 10 |
1 2 1 |
2 1 2 |
3 5 1 |
0 0 1 |
1 0 0 |
0 1 1 |
|
4 5 |
|
|
10 35 |
2 3 |
4 3 |
4 8 |
0 0 |
0 0 |
0 0 |
第2步
|
|
|
3 |
|
|
0 |
0 |
1 |
|
|
-3 |
4 |
|
|
1 |
0 |
0 |
|
|
1 |
6 |
|
|
0 |
1 |
0 |
|
|
|
-6 |
|
|
0 |
0 |
0 |
|
|
|
3 |
|
|
0 |
0 |
0 |
第3步
|
|
-2 |
|
|
1 |
0 |
0 |
|
|
-3 |
|
|
0 |
1 |
0 |
|
|
1 |
|
|
0 |
0 |
1 |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
第4步
|
|
-2 |
|
0 |
1 |
0 |
|
|
|
-3 |
|
0 |
0 |
1 |
|
|
|
-1 |
|
1 |
0 |
0 |
|
|
|
|
-15 |
0 |
0 |
0 |
-1 |
相应的目标函数值等于![]() .第4步得到一极小可行解
.第4步得到一极小可行解
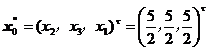
而![]() ,且目标函数
,且目标函数![]() 的值等于-15.所以所要求的目标函数
的值等于-15.所以所要求的目标函数![]() 的值为+15.
的值为+15.
[改进的单纯形法] 单纯形法和改进的单纯形法的主要区别在于单纯形法用消去公式变换单纯形表中的所有元素,而改进的单纯形法只要用同样的公式变换基底![]() 的逆矩阵
的逆矩阵![]() 的元素,一般来说改进的单纯形法计算量比原单纯形法的计算量小.
的元素,一般来说改进的单纯形法计算量比原单纯形法的计算量小.
为了便于使用改进的单纯形法,引进两个新变量(称为“多余”变量)![]() 和
和![]() 如下:
如下:
将一般的线性规划问题(4)~(6)改为等价问题:极大化
满足条件
![]() (7)
(7)
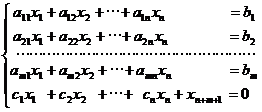 (8)
(8)
 (9)
(9)
并且假设所有的![]() .
.
再定义“多余方程”:
![]()
其中
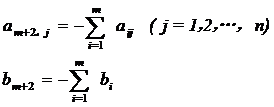 (10)
(10)
引进人工变量![]() ,命
,命![]() ,那末可将改进的问题(7)~(9)改写为极大化
,那末可将改进的问题(7)~(9)改写为极大化
![]() (11)
(11)
满足条件
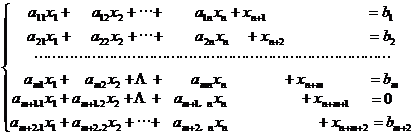 (12)
(12)
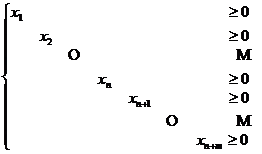 (13)
(13)
由(10)和(12)有
![]()
由于![]() ,显然
,显然![]() 不能是正的.
不能是正的.
改进的单纯形法就是通过解改进的线性规划问题(11)~(13)来得到一般的线性规划问题(4)~(6)的解.
从(12)中分离出所需要的系数并排成![]() 矩阵如下:
矩阵如下:
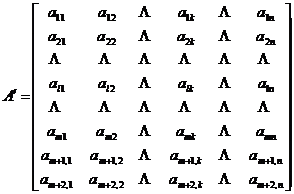
将![]() 的诸列矢量记为
的诸列矢量记为![]() .
.
命![]() 为
为![]() 矩阵
矩阵
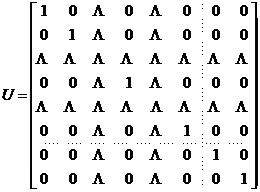
![]() 的前
的前![]() 行和
行和![]() 列表示初始基底B的逆矩阵.命
列表示初始基底B的逆矩阵.命![]() 表示U的第i个行矢量,
表示U的第i个行矢量,![]() 表示U的变换后的第i个行矢量.
表示U的变换后的第i个行矢量.
将矩阵U和初始解![]() 排成如表5中初始表的形式.计算步骤如下:
排成如表5中初始表的形式.计算步骤如下:
第一阶段 在解中有正值的人工变量时:
(1) 如果![]() ,则计算
,则计算
![]()
并进行(2).
如果![]() ,则进行第二阶段(1).
,则进行第二阶段(1).
表 5
|
|
|
解中变量 的标号 |
变量的值 |
矩阵U |
|
|
|
初 始 表 |
1 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
变 换 |
1 2
|
|
|
|
|
|
|
表 |
|
|
|
|
|
|
(2)如果所有的![]() ,那末
,那末![]() 达到它的极大值,因此问题(7)~(9)不存在可行解.
达到它的极大值,因此问题(7)~(9)不存在可行解.
若至少有一 ![]() ,则将对应于
,则将对应于
![]()
的变量![]() 引入解中.若有几个
引入解中.若有几个![]() 等于极小值,则选择标号
等于极小值,则选择标号![]() 最小的
最小的![]() .
.
(3)计算
![]()
把对应于
![]() (
(![]() )
)
的变量![]() 从解中消去.若有几个
从解中消去.若有几个![]() 对应于极小值,则选择标号
对应于极小值,则选择标号![]() 最小的
最小的![]() .
.
(4)基本可行解中变量的新值由公式
![]()
![]()
![]()
得到.矩阵![]() 的新元素由变换
的新元素由变换
![]()
![]()
![]()
得到.在这个变换下![]() 的第
的第![]() 和
和![]() 列不变.
列不变.
重复以上步骤,直到确定没有可行解存在或者![]() .如果
.如果![]() ,则进行第二阶段.
,则进行第二阶段.
第二阶段 在解中无正值的人工变量时:
(1) 此时![]() .计算
.计算
![]() (
(![]() )
)
(2) 如果所有的![]() ,那末
,那末![]() 达到它的极大值,相应的基本可行解是最优解.
达到它的极大值,相应的基本可行解是最优解. ![]() 是要极小化的目标函数的真值.
是要极小化的目标函数的真值.
如果至少有一个![]() ,则将对应于
,则将对应于
![]()
的变量![]() 引入解中.若有几个
引入解中.若有几个![]() 对应于极小值,则选择标号
对应于极小值,则选择标号![]() 最小的
最小的![]() .
.
(3) 计算
![]()
把对应于
![]() (
(![]() )
)
的变量![]() 从解中消去.若有几个
从解中消去.若有几个![]() 对应于极小值,则选择标号
对应于极小值,则选择标号![]() 最小的
最小的![]() .如果所有的
.如果所有的![]() ,那末得到一解其对应的目标函数值可以任意大.
,那末得到一解其对应的目标函数值可以任意大.
(4) 变量的新值由公式
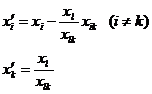
得到.矩阵U的新元素由变换
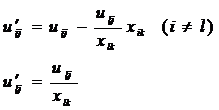
得到.
重复以上步骤直到确定一个最优解其对应的目标函数值是有限的或者是无限的.
(11)~(13)的初始解和以上步骤可以按表5所安排的计算步骤实现.
注意,若矩阵A的某一列是单位矢量且其对应的价格系数为零(例如某些松驰矢量),则该矢量可作为基底矢量,这样可以避免使用全人工基底减少迭代次数.
例2 极大化
![]()
满足条件
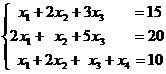
和 ![]()
解 这里![]() .相应的极小化问题的目标函数为
.相应的极小化问题的目标函数为
![]()
上述问题的全人工基底的改进单纯形法为:极大化满足条件
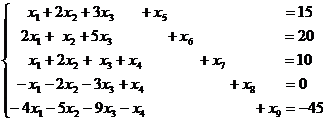
第4行的前面四个变量的系数等于原来要极小化的目标函数![]() 的表达式中的相应的
的表达式中的相应的![]() ,第5个方程的变量
,第5个方程的变量![]() 的系数和方程的右端常数项由公式(10)得到.
的系数和方程的右端常数项由公式(10)得到.
矩阵![]() 和
和![]() 分别为
分别为
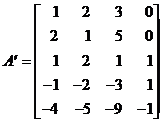

初始表和相继的迭代过程如表6所示.
表 6
|
|
|
解中变量 的标号 |
变量的值 |
矩阵 |
|
第一阶段 |
|
|
初 始 表 |
1 2 3 |
5 6 7 |
15 20 10 |
|
|
3 5 1 |
|
|
4 5 |
8 9 |
0 -45 |
|
|
|
|
|
|
1 次 迭 代 |
1 2 3 |
5 3 7 |
3 4 6 |
|
0 0 0 0 0 0 |
|
|
|
4 5 |
8 9 |
|
|
|
|
||
|
第 2 次 迭 代 |
1 2 3 |
2 3 7 |
|
|
0 0 0 0 0 0 |
0 0 1 |
|
|
4 5 |
8 9 |
+15
|
|
|
|
|
|
|
第 3 次 迭 代 |
1 2 3 |
2 3 7 |
|
|
0 0 0 0 0 0 |
|
|
|
4 5 |
8 9 |
|
|
|
|
|
|
|
第 4 次 迭 代 |
1 2 3 |
2 3 1 |
|
|
0 0 0 0 0 0 |
|
所有的 最优解 |
|
|
|
|
|
|
|
目标函数的值: |
|
[拉格朗日乘数法] (见第五章§3,十)将条件极值问题化为无条件极值问题后可以利用§2和§3无条件极值问题的解法求解.
[惩罚函数法(SUMT方法)]
![]() 外点法(SUMT方法之一) 考虑一般形式的条件极值问题
外点法(SUMT方法之一) 考虑一般形式的条件极值问题
![]() (14)
(14)
其中
![]()
而![]() 为定义在
为定义在![]() 上的连续函数.其迭代程序如下:
上的连续函数.其迭代程序如下:
(1) 选取![]() (例如取
(例如取![]() ),预先给定的允许误差为
),预先给定的允许误差为![]() ,令
,令![]() .
.
(2) 求无条件极值问题的最优解![]() :
:
![]()
其中
![]()
(3) 若存在某![]() ,满足
,满足
![]()
则取![]() (例如
(例如![]() 或5),令
或5),令![]() ,进行(2);否则就得到条件极值问题(14)的最优解的近似解
,进行(2);否则就得到条件极值问题(14)的最优解的近似解![]() .
.
![]() 内点法(SUMT方法之二) 考虑一般形式的条件极值问题
内点法(SUMT方法之二) 考虑一般形式的条件极值问题
![]()
![]() (15)
(15)
其中
![]()
且
![]()
(![]() 表示空集),而
表示空集),而![]() 为定义在
为定义在![]() 上的具有一阶连续偏导数的函数,其迭代程序如下:
上的具有一阶连续偏导数的函数,其迭代程序如下:
(1) 选取![]() (例如取
(例如取![]() ),预先给定的允许误差为
),预先给定的允许误差为![]() .
.
(2) 求![]() 的内点
的内点![]() ,令
,令![]() .
.
(3) 以![]() 作为初始点,对
作为初始点,对![]() 在保持可行性的情况下,使用求解无条件极值问题的方法求解:
在保持可行性的情况下,使用求解无条件极值问题的方法求解:
![]()
其中
![]()
或
![]()
(4) 当取![]() 时,检验是否满足判别准则:
时,检验是否满足判别准则:
![]()
而当取![]() 时,检验是否满足判别准则:
时,检验是否满足判别准则:
![]()
若满足判别准则,则得到条件极值问题(15)的最优解的近似解![]() ;否则,取
;否则,取![]() (例如
(例如![]() 或5),令
或5),令![]() ,进行(3).
,进行(3).
附:内点求法
设
![]()
![]()
其中![]() 是定义在集合
是定义在集合![]() 上的连续函数.
上的连续函数.
所谓求内点就是求出一点![]() ,其迭代程序如下:
,其迭代程序如下:
(1) 任取一点
![]() ,及数
,及数![]() (例如
(例如![]() ),令
),令![]() .
.
(2) 求出集合![]() 及
及![]() :
:
![]()
![]()
(3) 若![]() ,则得到内点
,则得到内点![]() ,否则,进行(4).
,否则,进行(4).
(4) 在保持对集合![]() 的可行性的情况下极小化
的可行性的情况下极小化![]() ,即
,即
![]()
其中
![]()
![]()
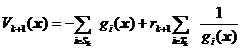 (
(![]() )
)
设![]() 为上述问题的最优解的近似解.
为上述问题的最优解的近似解.
(5) 取![]() (例如
(例如![]() ,
,![]() 或5),令
或5),令![]() ,进行(2).
,进行(2).