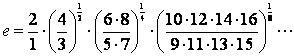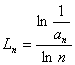§2   级数的收敛与运算

 

一、数项级数收敛的判别法

 

    1．基本概念与基本性质

    [级数的基本概念]设 ,,是一个无穷序列,符号

称为无穷级数,简称级数,记作.an称为级数的一般项.

An= a1+a2+            (n=1,)

称为级数的第n个部分和.若当n∞时，部分和序列{An}具有有穷或无穷（但有确定的正号或负号的）极限A：

A=An=

则称A为级数的和，并写成

A= a1+a2+

若级数具有有穷和，则称级数为收敛的，否则，即级数和等于±∞，或不存在，则称级数为发散的.

    [级数的基本性质]

    1°  弃去级数前面的有限项或在级数前面加进有限项，并不影响级数的收敛与发散的性质.

    2°  若级数收敛，则它的第m项后的余项的和数

am=am+1+am+2+

当m∞时趋于零.

    3°  若级数收敛，c是任一常数，则级数也收敛，并有

=c

    4°  若与都收敛，则也收敛，并有

=±

    [柯西准则]  级数收敛的充分必要条件是：对任意的ε>0，都存在正整数N=N(ε),使得当nN时，对一切正整数p，下列不等式成立：

    [级数收敛的必要条件]  级数收敛的一个必要条件是：一般项an趋于零，即an=0.

    2. 同号级数收敛判别法

    设

                            (1)

与                                                         (2)

为两个同号级数（即每一项符号相同的级数，当都是正号时，称为正项级数），这类级数的收敛判别法见下表.

名  称

条  件

级数的收敛性

收  敛

发   散

比较判别法

I

当n>N时，

0≤a­n≤b­­n

若级数(2)收敛，则级数(1)收敛

若级数(1)发散，则级数(2)发散

II

(0≤K≤+∞)

(bn≠0)

当K<+时，若级数(2)收敛，则级数(1)收敛

当K>0时，若级数(2)发散，则级数(1)发散

III

当n>N时，

≤

(an­≠0,bn≠0)

若级数(2)收敛，则级数(1)收敛

若级数(1)发散，则级数(2)发散

IV

当n→∞时，

  an­～bn

级数(1)和(2)同时收敛

级数(1)和(2)同时发散

V

an­=O*()

当p>1时

当p≤1时

达兰贝尔判别法

an>0(n=1,2,…)=q

当q<1时

当q>1时

柯西判别法

an­≥0(n=1,2,…)

当q<1时

当q>1时

拉阿伯判别法

an>0(n=1,2,…)

=p

当p>1时

当p<1时

高斯判别法

an>0(n=1,2,…)

其中有界：

≤L,>0

当λ>1时，或者当λ=1，而μ>1时

当λ<1时，或者当λ=1，而μ≤1时

柯西积分判别法

f(x) (x≥1)

为非负不增函数

与

同时收敛

与

同时发散

 对数判别法

an>0(n=1,2,…)

设

当n>N()，

>0时，

当n≥N()，

>0时，

 

    3. 变号级数收敛判别法

    [级数的绝对收敛性]  若级数

                                     (3)

收敛，则变号级数（即正负项可以任意出现的级数）

                                       (4)

也收敛，并称级数（4）为绝对收敛.

若级数（4）收敛，而级数（3）发散，则称（4）为条件收敛（非绝对收敛）.

要确定级数的绝对收敛性，只须把上面关于同号级数的收敛判别法应用到正项级数上去.但对发散性判别法必须当心，虽然级数是发散的，级数也仍然可以收敛（非绝对收敛），仅仅柯西判别法与达兰贝尔判别法是例外.

绝对收敛级数的和等于级数的所有正项组成的级数的和减去级数所有负项的绝对值组成的级数的和.

    [黎曼定理]  设为条件收敛级数，若适当的变更项的次序，则可收敛于任一给定的数（有限或无限）.

    [达兰贝尔判别法]  若变号级数满足条件

=l

则当l<1时，绝对收敛；当l >1时，发散.

    [莱布尼茨判别法]    若交错级数

满足条件：（i）cn≥cn+1(n=1,2,…),(ii) cn=0,则该级数收敛（一般说来，非绝对收敛）.对于级数的余项

有以下估计：

而且余项的符号与其第一项的符号相同，其绝对值比第一项绝对值小.

    [狄利克莱判别法]  若部分和An=有界，且当n时，bn单调地趋于零，则级数收敛.

    [阿贝耳判别法]  若级数收敛，且数bn(n=1,2,…)构成一单调有界序列：

|bn|≤K   (n=1,2,…)

则级数收敛.

 

二、函数项级数收敛的判别法

 

    1. 收敛与一致收敛

[收敛与收敛区域]  设un(x)(n=)都是定义在某区间[a,b]上的函数，则称

为定义在[a,b]上的函数项级数.若对区间[a,b]上的每点的部分和

Sn(x)=

当n→∞时，都有极限S(x)，即

Sn(x)= =S(x)

则称函数项级数在区间[a,b]上是收敛的，函数S(x)是它的和，区间[a,b]是收敛区域.函数

rn(x)=

称为余项.显然在收敛区域上的每点x，都有

rn(x)=0

也就是说，对任意给定的ε>0与收敛区域[a,b]上的每点x，都存在一个自然数N(ε,x)(N的大小不但与给定的正数ε有关，而且与x的数值有关)，使得当n≥N时，都有

|rn(x)|<ε或||<ε

    [一致收敛]  设函数项级数

对区间[a,b]上每点都收敛，它的和是S(x).

若对给定的ε0，都存在一个只与ε有关而与x的数值无关的自然数N(ε),使得当n≥N时，不等式

|rn(x)|<ε或||<ε

对于[a,b]上的一切x都成立，则称函数项级数在区间[a,b]上一致收敛，即部分和Sn(x)一致收敛于级数的和S(x).

由一致收敛的定义可知函数项级数在某区间[a,b]上一致收敛比在[a,b]上点点收敛的要求高.在某区间[a,b]上一致收敛的一个函数项级数在[a,b]上一定点点收敛，但在区间[a,b]上点点收敛的函数项级数在[a,b]上不一定一致收敛.

    2. 一致收敛判别法

    [柯西准则]  级数在区间[a,b]上一致收敛的充分必要条件是：

对任意给定的ε>0，都存在一个只与ε有关而与x无关的自然数N=N(ε)，使得当nN时，不等式

对一切自然数p以及区间[a,b]上一切点x,都成立.

    [外尔斯特拉斯判别法]  对于级数，若有收敛的数项级数存在，使得对区间[a,b]上一切点x，不等式

成立，则级数在区间[a,b]上绝对且一致收敛

    [阿贝耳判别法]  若级数在区间[a,b]上一致收敛，函数序列{(x)}对每个x是单调序列，而且对任意的x与n都是有界的：

|

则级数

(x)

在区间[a,b]上一致收敛.

    [狄利克莱判别法]  若级数的部分和对任意的x与n都是有界的：

函数序列{vn(x)}（对每个x）是在区间[a,b]上一致趋向于零的单调序列.则级数

(x)

在区间[a,b]上一致收敛.

 

3．函数级数的运算及其条件

 

运  算

表 达 式

条  件

级数和的连续性

在[a,b]上连续

(i)在[a,b]上连续，

(ii)在[a,b]上一致收敛

逐项相加减

=

(a≤x≤b)

，在[a,b]上都收敛

相乘

      =

其中

 

   

      

       (a≤x≤b)

,在[a,b]上都收敛，并且至少有一个绝对收敛

逐项取极限

     =

      (a≤≤b)

(i)(n=1,)，

        为有限值，

(ii) 在[a,b]上一致收敛

逐项微分

(a≤x≤b)

(i)定义在[a,b]上，

   而且有连续的导数，

(ii) 在[a,b]上收敛，

(iii)在[a,b]上一致收敛

逐项积分

=，

=

对于[a,b]上的一切点x一致成立

(i) 在[a,b]上连续(或

   可积)，

(ii) 在[a,b]上一致收敛

 

三、二重级数

 

    [二重级数]  已知由两个自然数附标决定的无穷数集

               

把它们排列成无穷矩阵的形状：

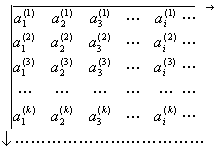
这种矩阵称为带两个附标的元素的无穷矩阵.

称为二重级数.

限于前m行与前n列，考虑有穷和数

这和数称为二重级数的部分和.

如果存在二重极限

A=

这极限是有穷的或无穷的（但有确定的正号或负号），那末称这极限为二重级数的和，记作

A=

若级数具有有限和，则称它是收敛的，否则，称它是发散的.

二重级数收敛的一个必要条件是一般项趋于零，即

=0

    [累级数]  如果在无穷矩阵中把每一行单独地相加起来，就得到行级数

再把所有行级数相加起来（先按列后按行相加），即

它称为累级数.如果先按行后按列把给定的无穷矩阵的项相加，就得到第二种累级数

若累极限

=

存在，则称累级数收敛，具有和.若累极限

=

存在，则称累级数收敛，具有和.

    [二重级数与累级数的关系]  如果(i)二重级数收敛，(ii)行级数收敛，那末累级数收敛，并且有与二重级数相同的和

=A=

对于第二种累级数有类似结论（参考§1，三，2）.

    [正项级数]

    1°  设，则级数收敛的充分必要条件是它的部分和有界.

    2°  设，如果三个级数

，，

中的一个级数收敛，那末其余两个级数也收敛，并且具有相同的和.

    3°  设，二重级数与简单级数由相同的项组成.在这种情形下，从一个级数的收敛性可推出另一个级数的收敛性，并且二者的和相等.

    [绝对收敛级数]

    1°  如果由级数的项的绝对值所组成的级数收敛，那末级数也收敛.

如果级数收敛，那末级数称为绝对收敛级数.如果级数收敛，而级数发散，那末级数称为条件收敛级数.

    2°  若级数绝对收敛，则行（或列）级数都绝对收敛.此外，由行（或列）级数的和所组成的级数也绝对收敛，并且与二重级数有相同的和.

    3°  如果由同样的项组成二重级数与简单级数，那末从它们中一个级数的绝对收敛性可推出另一个级数的绝对收敛性，并且二者的和相等.

    4°  绝对收敛的二重级数具有可交换性，即任意改变它的求和次序后级数仍然收敛，并与原级数有相同的和.

    5°  如果累级数的绝对值级数是收敛级数，那末不仅累级数本身收敛，而且累级数也收敛，并且二者的和相等.

    6°  如果简单级数绝对收敛，把它的项任意排列成带两个附标的元素的无穷矩阵的形状后，就可以用累级数或来代替级数.

二重级数的基本概念及性质可推广到多重级数上去.

 

四、无穷乘积

 

    [基本概念]  设

是一个给定的无穷序列,则记号

=, qn≠0    (n=1,)

称为无穷乘积.

称为部分乘积.如果当n→∞时部分乘积序列{Pn}具有有穷的或无穷的（但有确定的正号或负号）极限

Pn=P

则P称为无穷乘积的值，记作

P==,   qn≠0(n=1,)

若无穷乘积具有非零有穷值P,则称为收敛的，否则称为发散的.若P=0，则称为发散于零.

为使无穷乘积的值等于零，只要乘积的因子中有一个是零就够了，在后面的讨论中，总是假定qn≠0(n=1, ).

称为无穷乘积的余乘积.

    [无穷乘积收敛判别法]

    1°  无穷乘积收敛的一个必要条件是：

πm=1或qn=1

式中πm=.

    2°  无穷乘积收敛的充分必要条件是：级数收敛.设L是前面级数的和，则P=eL.

    3°  设qn=1+an(n=1,2,…)，对充分大的n，若有an>0(或an<0)，则=收敛的充分必要条件是：级数收敛.

    4°  若级数与级数同时收敛，则=收敛.

    5°  无穷乘积或具有零值的充分必要条件是：级数或的和为.

特别，如果an<0且级数发散，或级数收敛而级数发散，那末无穷乘积具有零值.

    6°  无穷乘积绝对收敛的充分必要条件是：级数绝对收敛.

    [函数项无穷乘积的一致收敛]  如果函数序列

Pm(x)=            (m=1,)

一致收敛，并且极限不恒为零，那末称函数项无穷乘积

一致收敛.

如果在某一区间上一致收敛，且,那末无穷乘积也在该区间上一致收敛.

    [无穷乘积展开式]

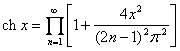
   (|x|<1)

                                            (其中γ为欧拉常数)

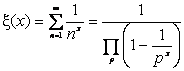
（其中p跑遍一切素数，ξ(x)称为黎曼ξ函数.）