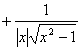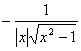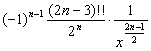§3   微  分

 

一、单变量函数的微分

 

    1. 基本概念

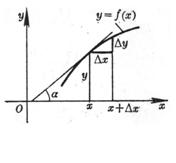
[导数的定义及其几何意义]  设函数y=f(x)当自变量在点x有一改变量时,函数y相应地有一改变量 ,那末当趋于零时,若比的极限存在(一确定的有限值)，则称这个极限为函数f(x)在点x的导数,记作

这时称函数f(x)在点x是可微分的函数(或称函数f(x)在点x可微)。

在几何上,函数f(x)的导数是函数y=f(x)表示的曲线在点x的切线的斜率,即

=

式中α为曲线在点x的切线与x轴的夹角(图5.1)。

    [单边导数]

=

及

=

分别称为函数f(x)在点x的左导数和右导数。

导数存在的充分必要条件是:

=

    [无穷导数]  若在某一点x有

=±∞

则称函数f(x)在点x有无穷导数。这时函数y=f(x)的图形在点x的切线与x轴垂直(当=

+∞时,函数f(x)的图形在点x的切线正向与y轴方向一致,当=－∞时,方向相反)。

    [函数的可微性与连续性的关系]  如果函数y=f(x)在点x有导数，那末它在点x一定连续。反之,连续函数不一定有导数,例如

    1°　函数y=|x|在点x=0连续,在点x=0,左导数=－1,右导数 =1,而导数不存在(图5.2)。

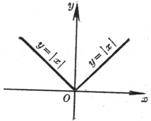                                                图5.2                                                   图5.3

    2°　函数

                     y=f(x)=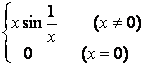 

在点x=0连续,但在点x=0左右导数都不存在(图5.3)。

    2. 求导数的基本法则

[四则运算求导公式]　若c为常数,函数u=u(x), 都有导数,则

          =0               =c

                

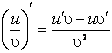          （≠0）

[复合函数的导数]  若y=f(u),u=都有导数,则

=

[反函数的导数]  如果函数y=f(x)在点x有不等于零的导数,并且反函数x=f^－1(y)在点y连续,那末  存在并且等于，即

=

[隐函数的导数]  假定函数F(x,y)连续,并且对于每个自变量都有连续的偏导数,而且，则由

F(x,y)=0

所决定的函数y=f(x)的导数

=＝

式中＝，＝(见本节，四)。

[用参数表示的函数的导数]  设方程组

　（α<t<β）

式中和为可微分的函数,且,则由隐函数存在定理(本节,四,1)可把y确定为x的单值连续函数

y=

而函数的导数可用公式

＝

求得。

[用对数求导数法]  求一函数的导数,有时先取其对数较为便利,然后由这函数的对数求其导数。

例  求

的导数。

解  两边各取对数,得

lny=pln(x－a)＋qln(x－b)－rln(x－c)

左边的lny为y的函数,而y又为x的函数,故应用求复合函数的导数的法则得到

由此得

所以

3.函数的微分与高阶导数

[函数的微分]  若函数y=f(x)的改变量可表为

＝A(x)dx+o(dx)

式中dx=Δx，则此改变量的线性主部A(x)dx称为函数y的微分,记作

dy=A(x)dx

函数y=f(x)的微分存在的充分必要条件是:函数存在有限的导数=,这时函数的微分是

dy=dx

上式具有一阶微分的不变性,即当自变量x又是另一自变量t的函数时,上面的公式仍然成立.

[高阶导数]  函数y=f(x)的高阶导数由下列关系式逐次地定义出来(假设对应的运算都有意义)：

 =      

[高阶微分]  函数y=f(x)的高阶微分由下列公式逐次定义：

= 

式中.并且有

=

及                                

[莱布尼茨公式]  若函数u=及=有n阶导数(可微分n次),则

式中,,为二项式系数。

同样有

式中                                            ，

更一般地有

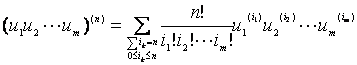
式中m，n为正整数。

[复合函数的高阶导数]  若函数y=f(u),u=有l阶导数，则

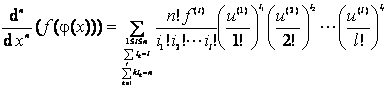
式中                   

，

 

 

[基本函数的导数表]

 

[简单函数的高阶导数表]

 

f(x)
	m(m－1)…(m－n+1) (当m为整数且n>m时，=0)
	这里(2n+1)!!=(2n+1)(2n－1)
	(a>0)
shx	shx(n为偶数)，chx(n为奇数)
chx	chx(n为偶数)，shx(n为奇数)

 

4.数值导数

当函数用图形或表格给出时,就不可能用定义求出它的导数,只能用近似方法求数值导数.

[图解微分法]  适用于用图形给出的函数求导数,例如机械设计中已知s－t图,求图,  a－t图等,其基本步骤如下：

(1)        将原坐标系Oxy沿y轴负方向平移一段距离得坐标系 (图5.4).

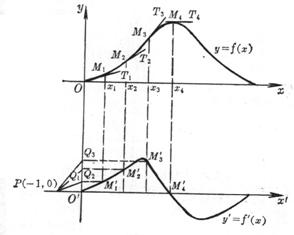
图5.4

(2)  过曲线y=f(x)上点M₁(x₁,y₁)作切线M₁T₁ .在坐标系内,过点P(－1,0)作PQ₁平行于M₁T₁交y轴于点Q₁ ,那末点Q₁ (点)的纵坐标就是导数.以Q₁的纵坐标为纵坐标,x₁为横坐标作出点.

(3)  在曲线y=f(x)上取若干个点M₁,M₂,,在曲线弯曲程度较大处点取得密些.仿上作法,在坐标系内得到相应点,,,顺次连成光滑曲线,即是导函数的图形.

[差商公式]  在实用中常使用下列简单的近似公式

,,…,

式中

   =          （函数f (x)在点a的１阶差分）

　   　  （函数f (x)在点a的２阶差分）

 ……………………………………

   （函数f (x)在点a的k阶差分）

在函数的数值表中,如果有误差,则高阶差分的偏差较大,所以用以上公式不宜计算高阶导数.

[用插值多项式求数值导数]  假定已经求出了函数y=f (x)的插值多项式P_n (x),它可以求导,则用近似,由

f(x)=P_n(x)+R_n(x)

略去余项,得

≈           ≈

等等.它们的余项相应为,,等等.

应当指出,当插值多项式P_n(x)收敛于f(x)时, 不一定收敛于f' (x).另外,当h缩小时,截断误差减小,但舍入误差却增加,因此,采用缩小步长的方法也不一定能达到提高精度的目的.由于用插值法求数值微分的不可靠性,在计算时,要特别注意误差分析,或者改用其他方法.

[拉格朗日公式]  (由拉格朗日插值公式得来,见第十七章,§2,三)

式中                                

                                    

                                    

     ()

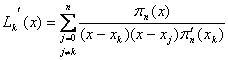
[马尔科夫公式]  (由牛顿插值公式得来,见第十七章,§2,二)

                           ()

特别,当t = 0时,有

              

              

               

              

[等距公式]

三点公式

≈

四点公式

≈

五点公式

≈

      

[用三次样条函数求数值导数]  这个方法能避免用插值法求数值导数的不可靠性.因为对于样条函数(曲线y=f(x)的三次样条函数S(x)的作法见第十七章,§2,四),当被插值函数f(x)有四阶连续导数,且h_i=x_i+1－x_i→0时,只要S(x)收敛于f(x),则导数一定收敛于,且S(x)－f(x)=O(H⁴)，－＝O(H³),,其中H是h_i的最大值,因此,可直接通过三次样条函数

      

求数值导数得

=

                         

   

                                      

式中      ,,   (i=0,1,2,)。

   若仅求样点x_i上的导数,则

                   

≈=

≈=

 

二、多变量函数的微分

 

[偏导数及其几何意义]  设二元函数

u=f(x,y)

当变量x有一个改变量Δx而变量y保持不变时,得到一个改变量

Δu=f(x+Δx,y)－f(x,y)

如果当Δx→0时,极限

=

存在,那末这个极限称为函数u=f(x,y)关于变量x的偏导数,记作或,也记作或,即

=====

类似地,可以定义二元函数u=f(x,y)关于变量y的偏导数为

=====

偏导数可以按照单变量函数的微分法则求出,只须对所论变量求导数,其余变量都看作常数.

偏导数的几何意义如下:

二元函数u=f(x,y)表示一曲面,通过曲面上一点M(x,y,u)作一平行于Oxu平面的平面,与曲面有一条交线,就是这条曲线在该点的切线与x轴正向夹角的正切,即=.同样,有= (图5.5).

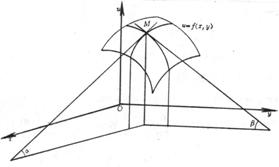
图5.5

偏导数的定义不难推广到多变量函数u=f(x₁,x₂,…,x_n)的情形.

[偏微分]  多变量函数u=f(x₁,x₂,…,x_n)对其中一个变量(例如x₁ )的偏微分为

也可记作.

[可微函数与全微分]  若函数u=f(x,y)的全改变量可写为

=+

式中A,B与Δx,Δy无关,,则称函数u=f(x,y)在点(x,y)可微分(或可微),这时函数u=f(x,y)的偏导数,一定存在,而且

=A, =B

改变量Δu的线性主部

=+dy

称为函数u=f(x,y)的全微分,记作

du=+dy                                 (1)

函数在一点可微的充分条件:如果在点(x,y)函数u=f(x,y)的偏导数存在而且连续,那末函数在该点是可微的.

公式(1)具有一阶微分的不变性,即当自变量x,y又是另外两个自变量t,s的函数时,上面的公式仍然成立.

上述结果不难推广到多变量函数u=f(x₁,x₂,…,x_n)的情形.

注意,在一个已知点,偏导数的存在一般说来还不能确定微分的存在.

[复合函数的微分法与全导数]

1° 设u=f(x,y),x=(t,s),y=(t,s),则

=+

=+

2° 设u=f(x₁,x₂,…,x_n),而x₁,x₂,…,x_n又都是t₁,t₂,…,t_m的函数,则

…………………………………………

3° 设u=f(x,y,z),而y=(x,t),z=(x,t),则

=

 

=

4° 设u=f(x₁,x₂,…,x_n), x₁= x₁(t), x₂= x₂(t), ,则函数u=f(x₁,x₂,)的全导数为

[齐次函数与欧拉公式]  如果函数f(x,y,z)恒等地满足下列关系式 

f(tx,ty,tz)=f(x,y,z)

则称f(x,y,z)是一个k次的齐次函数.对于这种函数,只要它可微,就有

   (欧拉公式)

注意,齐次函数的次数k可以是任意实数,例如,函数

就是自变量x及y的π次齐次函数.

[隐函数的微分法]  设F(x₁,x₂,…,x_n,u)=0,则

………………………

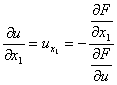
(参考本节,四).

[高阶偏导数与混合偏导数]  函数u=f(x₁,x₂,…,x_n)的二阶偏导数为,,…,和,,,…,后者称为混合偏导数.三阶偏导数为,,…, ,,,…。类似地可定义更高阶的偏导数.

关于函数乘积的混合偏导数有下面公式:设u,都是x₁,x₂,…,x_n的函数,则

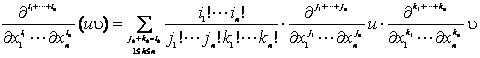
注意,混合偏导数一般与求导的次序有关,但是,如果两个同阶的偏导数,只是求导的次序不同,那末只要这两个偏导数都连续,它们就一定彼此相等.例如,如果在某一点(x,y)函数与都连续,那末一定有

(x,y)= (x,y)

[高阶全微分]  二元函数u=f(x,y)的二阶全微分为

d²u=d(du)=

或简记作

d²u=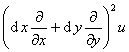

式中偏导数符号,经平方后出现,,,它们再作用到函数u=f(x,y)上,以下类同.

二元函数u=f(x,y)的n阶全微分为

dⁿu=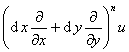

多变量函数u=f(x₁,x₂,…,x_m)的n阶全微分为

dⁿu=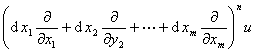

[偏导数的差分形式]

(表中h为x轴方向步长,l为y轴方向步长)

图  示								差 分 公 式
图  示								差 分 公 式
		图  示						差 分 公 式

 

 

三、函数行列式(或雅可比式)及其性质

 

设有n个自变量的n个函数

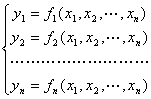                                     (1)

它们定义在某一n维区域D中,并关于自变量有连续偏导数,则由这些偏导数组成的行列式

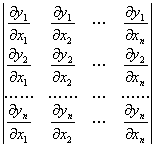
称为函数组(1)的函数行列式或雅可比式。记作

函数行列式具有与普通导数相似的一系列性质.

1°  除函数组(1)外,再取在区域P中有定义且有连续偏导数的函数组

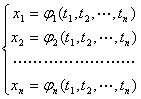
假设当点(t₁,t₂,)在P中变动时,对应点(x₁,x₂,)并不越出区域D,于是就可以通过x₁,x₂, 把y₁,y₂,看成是t₁,t₂,的复合函数.这时有

 =               (2)

它是一元的复合函数的微分法则

y=f(x),x=；=

的推广。

2°  特别是,如果令t₁=y₁,t₂=y₂,=y_n(换句话说,由新变量x₁,x₂,又回到旧变量y₁,y₂, ),则由(2)式得到

 =1

它是一元函数的反函数微分法则

y=f(x),  x==

的推广。

3°  设有n个自变量x₁,x₂,的m（m<n）个函数y₁,y₂, ：

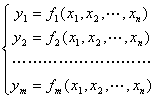
式中x₁,x₂,又是m个自变量t₁,t₂,的函数：

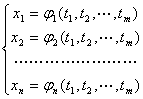
假设它们都有连续偏导数，那末y₁,y₂,作为t₁,t₂,的函数的函数行列式的表达式为

＝

等式右边的和式是从n个标号内每次取m个的一切可能组合而取遍的。

当m=1时,上面的公式就是普通的复合函数的微分公式

的推广.特别当n=3,m=2时,有

4°  设有2n个自变量的n个方程所组成的方程组

F_i(x₁,x₂,;y₁,y₂,)=0        (i=1,2,…,n)

假定

≠0

将y₁,y₂,看成由这方程组所确定的x₁,x₂,的函数,这时有

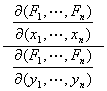
它是由F(x,y)=0所确定的隐函数y=f(x)的导数公式

的推广.

5°  函数行列式可作为面积(体积)的伸缩系数.

假定函数

u=u(x,y),  = (x,y)

在xy平面的某个区域上连续,并且有连续的偏导数,又假定在这个区域上

≠0

那末有                                  dud=dxdy

对更高维的空间有类似的表达式.

例  直角坐标与球面坐标的变换

x=rsincos,y=rsinsin,z=rcos

的函数行列式为

==

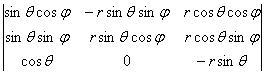这时             dxdydz=drdd= drdd