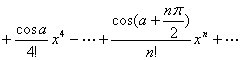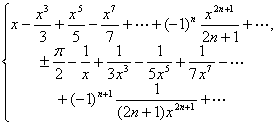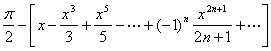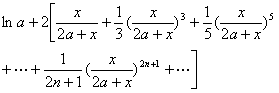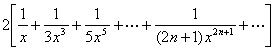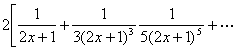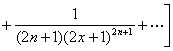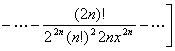四、隐函数
1. 单变量隐函数
对于由方程
F(x,y)=0
所确定的隐函数有下述定理:
[存在定理] 设函数F(x,y)在点M0(x0,y0)的某一邻域*R内定义并且满足下列条件:
(i) F(x,y)及其偏导数
在R内连续,
(ii) F(x0,y0)=0,
(iii)
≠0,
那末在点M0(x0,y0)的某一邻域
;
)
内有唯一的单值函数y=f (x)存在,具有下列性质:
1° F[x, f (x)]≡0,且f (x0)=y0,
2° 在区间()内函数f(x)连续,
3° 它在这区间内有连续的导数
.
[导数的计算]
(
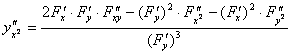≠0)
(≠0)
2. 多变量隐函数
对于由方程
F(x,y,z)=0
所确定的隐函数有下述定理:
[存在定理] 设函数F(x,y,z)在点P0(x0,y0,z0)的某一邻域R内定义并且满足下列条件:
(i)
F(x,y,z)及其偏导数,
在R内连续,
(ii) F(x0,y0,z0)=0,
(iii) (x0,y0,z0)
≠0,
那末在点P0(x0,y0,z0)的某一邻域
;;
)
内有唯一的单值函数z=h(x,y)存在,具有下列性质:
1° F[x,y,h(x,y)]≡0,且h(x0,y0)= z0,
2° 函数h(x,y)连续,
3° 它有连续的偏导数
.
[导数的计算]
,
(≠0)
如果需要求所有一,二,
各阶的偏导数,只要将恒等式
F(x,y,z)=0
两边求一阶,二阶,三阶,...各阶的全微分,然后和全微分dz,d2z,
的定义形式对比,即得.
注意,对于由方程
F(x1,
,xn,y)=0
所确定的隐函数有类似结果.
3. 由方程组所确定的隐函数
对由方程组
(1)
所确定的隐函数有下述定理:
[存在定理] 设函数F(x,y,z)及G(x,y,z)在点P0(x0,y0,z0)的某一邻域R内定义,并且满足下列条件:
(i) F(x,y,z),G(x,y,z)及其所有偏导数都在R内连续,
(ii) F(x0,y0,z0)=0,G(x0,y0,z0)=0,
(iii) 行列式
J(x,y,z)=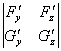
在点P0(x0,y0,z0)不等于零:J(x0,y0,z0)≠0.
那末在点P0(x0,y0,z0)的某一邻域
;;)
内有唯一的一组单值函数y=f(x),z=g(x)存在,具有下列性质:
1° F[x,f(x),g(x)]≡0,G[x,f(x),g(x)]≡0,且f(x0)=y0,g(x0)=z0,
2° 在区间()内函数f(x),g(x)连续,
3° 在这区间内有连续导数
.
[导数的计算] 将y和z看作x的隐函数,将方程组(1)对x微分得
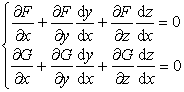
这是关于
及
的线性方程组,其行列式J≠0,由此可以解出及.
注意,对于由方程组
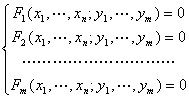
所确定的隐函数有类似的结果.
五、微分表达式中的变量替换
1.单变量函数
设y=f (x),并有一个含有自变量、因变量及其导数的表达式
H=F(x,y,
)
当作变量替换时,各导数可按下列方法计算:
[作自变量变换的情形] 设变换公式为
x=
这时
,
(1)
………………
[自变量和函数都作变换的情形] 设变换公式为
x=
,y=
式中t为新的自变量,u为新的函数.
这时,由复合函数的微分法则得到
,
…………………………
把这些式子代入公式(1),即得结果.
2. 多变量函数
[作自变量变换的情形] 设z=f (x,y),并有一个含有自变量、因变量及其偏导数的表达式
H=F(x,y,z,
, 
,
,…)
变换公式为
x=
,y=
式中u和
为新的自变量,则偏导数, 由下列方程确定:
=
+
其它高次偏导数也可仿此求出.
[自变量和函数都作变换的情形] 设变换公式为
x=
,y=
,z=
其中u, 为新的自变量, w=w(u,v)为新的函数,则偏导数, 由下列方程确定:
+
)+
+
)=
+
其他高次偏导数也可仿此求出.
注意,当H内出现的不是个别的偏导数,而是已给阶次的全部偏导数,那末求逐次偏导数时利用全微分比较方便.
六、微分学的基本定理(中值定理)
|
|
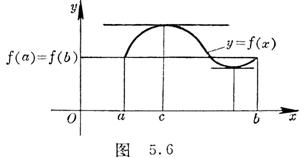
[洛尔定理] 如果(i)函数f (x)定义在闭区间[a,b]上而且是连续的,(ii)在开区间(a,b)内存在有限导数,(iii)在区间的两端点处函数值相等:
f (a)= f (b).那末在a与b之间至少存在一点c,使
=0.即曲线y= f (x)在点(c, f
(c))处的切线是水平的(图5.6).
特别,若f (a)= f (b)=0,洛尔定理可简述如下:在一个函数的两个根之间,它的一阶导数至少有一个根.
注意,函数f (x)须在闭区间[a,b]上连续,并且在开区间(a,b)内点点要有导数存在,这对于定理的结论的正确性是很要紧的.例如函数
f (x)=
在区间[0,1]上,除去在x=1时有间断以外满足定理的一切条件,但在(0,1)内处处都是=1.又例如由等式f (x)=x(
)及f (x)=
(
)所定义的函数,在这区间内除去当x=
时(双边的)导数不存在以外,它也满足定理的一切条件,可是导数在左半区间内等于+1,而在右半区间内等于
.
定理的条件(iii)也是很重要的,例如函数f (x)=x在区间[0,1]上,除去条件(iii)以外满足定理的一切条件,而它的导数处处是=1.
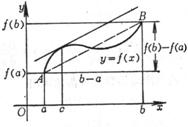
[中值定理] 如果(i) f (x)定义在闭区间[a,b]上而且是连续的,(ii) 在开区间(a,b)内存在有限导数,那末在a与b之间至少存在一点c,满足等式
= (a<c<b)
(1)
|
图5.7 |
即曲线y= f (x)在点(c, f (c))处的切线与弦AB平行(图5.7).这个定理也称为有限改变量定理或拉格朗日定理.
(1)式也常写成以下几种形式:
f (b)
f (x+Δx)
Δx (x<c<x+Δx)
Δy= f (x+Δx)
(
)
由中值定理可得
定理 如果在区间[a,b]上的每一点都有=0,那末函数f(x)在这个区间上是一个常数.
[柯西定理] 如果(i)函数f(t)及g(t)在闭区间[a,b]上连续,(ii)在开区间(a,b)内有有限导数,(iii)在区间(a,b)内
≠0.那末在a与b之间至少存在一点c,使
|
图5.8 |
=
(a<c<b)
这公式称为柯西公式(图5.8).柯西定理常称为微分学的广义中值定理,因g(t)=x时,这个公式就是公式(1).
[多变量函数的中值定理]
如果(i)函数f(x,y)定义在闭区域
上并且连续,(ii)在这区域内部(即在它的所有内点)有连续的偏导数
,
,今考察D中的两点
M0(x0,y0)及M1(x0+Δx,y0+Δy)
假设这两点能用全部位于D区域内的直线段M0M1来连接,则下面的公式成立:
Δf(x0,y0)=f(x0+Δx,y0+Δy)
=
(0<θ<1)
由中值定理可得
定理 若在闭连通区域D*内连续的函数f(x,y),在此区域内偏导数都等于零,即
==0,
则这函数在区域D内必为常数.
七、泰勒公式与泰勒级数
1. 单变量函数的泰勒公式
[泰勒局部公式] 如果函数f(x)满足条件:(i)在点a的某邻域
内有定义,(ii)在此邻域内有一直到
阶的导数
,
,(iii)在点a处有n阶导数
,那末f(x)在点a的邻域内可表成以下各种形式:
1°
f (a+h)= f (a)+
* 若区域的任意两点可以用一“折线”来连接，而该折线的一切点都在这区域中，这区域就称为连通区域.
=
(当h→0)
2° f (x)=
f (a)+
=
(当x→a)
特别,当a=0时,有
[马克劳林公式]
f (x)=
f (0)+
=
(当x→0)
[泰勒公式] 如果函数f (x)满足条件:(i)在闭区间[a,b]上有定义,(ii)在此闭区间上有一直到n阶的连续导数
,(iii)当a<x<b时有有限导数
,那末f(x)在闭区间[a,b]上可表成以下各种形式:
1° f(a+h)=
(a<a+h<b)
式中
Rn(h)=
(0<θ<1)
(拉格朗日型余项)
或
Rn(h)=
(0<θ<1) (柯西型余项)
2° f(x)=
(
)
式中
Rn(x)=
(a<ξ<b)
(拉格朗日型余项)
或
Rn(x)=
(0<θ<1)
(柯西型余项)
特别,当a=0时,有
[马克劳林公式]
f(x)=
()
式中
Rn(x)=
(a<ξ<b)
(拉格朗日型余项)
或
Rn(x)=
(0<θ<1) (柯西型余项)
[泰勒级数] 在带余项的泰勒公式2°中,如果把展开式进行到(
)的任意高的乘幂,则有
f(x)=f(a)+
不论它是否收敛,以及它的和是否等于f(x),都称它为函数f(x)的泰勒级数.()的乘幂的系数
f(a),
,
,…,
,…
称为泰勒系数.
[马克劳林级数] 在带余项的马克劳林公式中,如果展开式进行到x的任意高的乘幂,则有
f(x)=f(0)+
不论它是否收敛,以及它的和是否等于f(x),都称它为函数f(x)的马克劳林级数.x的乘幂的系数
f (0),
,
,…,
,…
称为马克劳林系数.
多项式的泰勒公式(秦九韶法)见第三章,§2,一.
2. 多变量函数的泰勒公式
[泰勒公式] 假定在某一点(x0,y0)的邻域D内二元函数f(x,y)有直到n+1阶为止的一切连续偏导数.分别给x及y以改变量h及k,使连结点(x0,y0)及(x0+h,y0+k)的直线段不越出D外,那末f (x,y)在D内可表成形式:
1° f (x0+h,y0+k)=
(0<θ<1)
式中符号
的意义如下:把
,
看作一个数(而不是看作微分运算的符号),并根据二项公式展开,得到
=
=
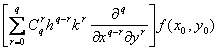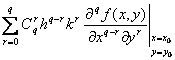
20
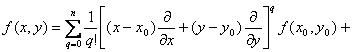
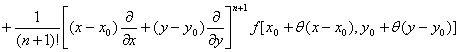
特别,当x0=0,y0=0时,得到
[马克劳林公式]
f (x,y)=
对二元以上的多变量函数有类似的公式.
[泰勒级数] 在上面泰勒公式2°中,如果把展开式进行到(
)和(
)的任意高的乘幂,则有
f (x,y)=
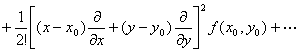
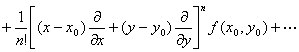
不论它是否收敛,以及它的和是否等于f(x,y),都称它为f(x,y)的泰勒级数.
[马克劳林级数] 在上面马克劳林公式中,如果把展开式进行到x,y的任意高的乘幂,则有
f (x,y)=
f (0,0)+
不论它是否收敛,以及它的和是否等于f (x,y),都称它为f (x,y)的马克劳林级数.
八、幂级数
1．单变量的幂级数
[定义] 下列形式的级数
（1）
（式中a0,a1,
都是实常数）称为x的幂级数.更一般地，级数
(式中a是一个实常数)也称为幂级数.
[绝对收敛] 如果级数（1）当x=
时收敛，那末对于满足|x|<||的任何x的值，级数（1）都绝对收敛.
[收敛半径与收敛区间] 对于任何一个幂级数，都有一个数R(0≤R<+∞),使得当|x|<R时，级数绝对收敛，当|x|>R时，级数发散.这个数R称为给定级数的收敛半径，区间(－R,R)称为它的收敛区间，而在区间的两个端点x=R和x=－R，级数可能收敛也可能发散.
收敛半径R可按柯西-阿达玛公式
或公式
R=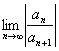
计算(若极限存在).
[阿贝尔定理] 若幂级数S(x)=
( |x|<R)在收敛区间的端点x=R处收敛，则
S(R)=
[内闭一致收敛] 若级数（1）的收敛半径等于R，则对任意满足0<
<R的，级数（1）在区间[
，]上一致收敛.
[连续] 幂级数的和在收敛区间内的每一点处都连续.
[逐项积分] 在级数（1）的收敛区间内的任何一点x，都有
式中S(x)表示级数（1）的和.
[逐项微分] 幂级数（1）的和S(x)在这个级数的收敛区间内的任一点上都可微.逐项微分级数（1）得到的级数
与（1）具有同样的收敛半径，并且这个级数的和就等于
.
[高阶导数] 若级数（1）有收敛半径R，则它的和S(x)在区间(
,R)内的任何一点都有任意阶导数，并且函数
（n=1,
）就是逐项微分级数（1）n次所得到的那个级数（它的收敛半径也同样是R）的和
=
（<x<R）
2．多变量的幂级数
[双变量的幂级数] 按变量x,y的正整数幂次排列的形如
（2）
的重级数称为双变量x,y的幂级数.
多变量幂级数的收敛范围的研究有很多地方与单变量的不同，但仍有
定理 若在x=x0,y=y0时级数（2）收敛，则当
|x|<|x0|,|y|<|y0|
时，级数也收敛.
[收敛范围] 如果M是两个变数x,y的区域，在其中各点上幂级数（2）都收敛，而在其外各点上幂级数（2）发散，在边界点上可能发散，也可能收敛.那末区域M称为幂级数（2）的收敛范围.
双变量的幂级数的收敛范围并不一定是|x|<R1，|y|<R2的形式，例如
1° 级数
的收敛范围是|x|<1，|y|<1.
2° 级数
处处收敛.
3° 级数
=1+x+
+xy+x2y+x3y+
+x2y2+
(=(1+x+
)[1+xy+
]=
)
的收敛范围是|x|<1，|xy|<1.
以上结果容易推广到多变量的幂级数中去.
3．函数的幂级数展开式
[幂级数的唯一性定理] 如果函数f(x)(或f(x,y))在x=0(或x=0,y=0)可以展开成幂级数
f(x)=
或 
那末这个幂级数就是它的马克劳林级数.
[幂级数的存在性定理]
1° 若函数f (x)在x=0具有任意阶导数，且当≤x≤R时
式中Rn(x)是马克劳林公式的余项，则函数f(x)在区间≤x≤R上可以展开成幂级数.实际上可以证明，存在由函数f(x)产生的马克劳林级数，它虽然收敛，但它的和却不等于f (x).
2° 若函数f (x,y)在点(0,0)具有任意阶偏导数，且当(x,y)是xy平面上某一区域M上的点时
式中Rn(x,y)是马克劳林公式的余项，则函数f(x,y)在区域M上可以展开成幂级数.
上述理论容易推广到二元以上的多变量函数的情形.
九、实数域上函数的幂级数展开式表
|
函 数 |
幂 级 数 展 开 式 |
收 敛 域 |
|
[二项式]
(m>0)
函 数 |
(当m为正整数时，只包含m+1项)
幂 级 数 展 开 式 |
收 敛 域 |
|
(m>0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m>0)
|
|
|
|
|
|
|
|
(p>0或q>0) |
|
|
|
[三角函数]
|
|
|
|
|
|
|
|
|
|
|
|
函 数 |
幂 级 数 展 开 式 |
收 敛 域 |
|
|
(式中Bn为伯努利数，下同，见231页的附表) |
|
|
|
|
0< |
|
|
(式中En为欧拉数，见231页的附表) |
|
|
|
|
0< |
|
[反三角函数]
|
|
|
|
|
|
|
|
|
|
|
|
函 数 |
幂 级 数 展 开 式 |
收 敛 域 |
|
[指数函数]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[对数函数]
|
|
x>0 |
|
|
|
0< |
|
|
|
x> |
|
|
|
|
|
|
|
|
|
(a>0)
|
|
|
|
|
|
|
|
函 数 |
幂 级 数 展 开 式 |
收 敛 域 |
|
|
|
|
|
|
|
|
|
|
|
0< |
|
|
|
|
|
|
|
0< |
|
[双曲函数]
shx |
|
|
|
chx |
|
|
|
thx |
|
|
|
cthx |
|
0< |
|
sechx |
|
|
|
|
|
|
|
函 数 |
幂 级 数 展 开 式 |
收 敛 域 |
|
cschx
[反双曲函数]
Arshx=
|
|
0<
|
|
Arshx |
|
|
|
Archx(双值)
Arthx=
Arcthx=
|
|
|
1
<1
1
>1
表中标*者应记牢.
附：伯努利数Bn和欧拉数En表
|
n |
Bn |
En |
|
1 |
|
1 |
|
2 |
|
5 |
|
3 |
|
61 |
|
4 |
|
1 385 |
|
5 |
|
50 521 |
|
n |
Bn |
En |
|
6 |
|
2 702 765 |
|
7 |
|
199 360 981 |
|
8 |
|
19 391 512 145 |
|
9 |
|
2 404 879 675 441 |
|
10 |
|
370 371 188 237 525 |
