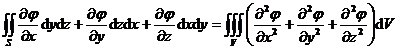§2
场论初步
一、
场论的基本概念及梯度、散度与旋度
[标量场] 空间区域D的每点M(x,y,z)对应一个数量值![]() (x,y,z),它在此空间区域D上就构成一个标量场,用点M(x,y,z)的标函数
(x,y,z),它在此空间区域D上就构成一个标量场,用点M(x,y,z)的标函数![]() (x,y,z)表示.若M的位置用矢径r确定,则标量
(x,y,z)表示.若M的位置用矢径r确定,则标量![]() 可以看作变矢r的函数
可以看作变矢r的函数![]() =
=![]() (r).
(r).
例如温度场u(x,y,z),密度场![]() ,电位场e(x,y,z)都是标量场.
,电位场e(x,y,z)都是标量场.
[矢量场] 空间区域D的每点M(x,y,z)对应一个矢量值r(x,y,z),它在此空间区域D上就构成一个矢量场,用点M(x,y,z)的矢量函数r(x,y,z)表示.若M的位置用矢径r确定,则矢量r可以看作变矢r的矢函数r(r):
r(r)=X(x,y,z)i+Y(x,y,z)j+Z(x,y,z)k
例如流速场 ![]() (x,y,z),电场E(x,y,z),磁场H(x,y,z)都是矢量场.
(x,y,z),电场E(x,y,z),磁场H(x,y,z)都是矢量场.
与标量场的情况一样,矢量场概念与矢函数概念,实质上是一样的.沿用这些术语(标量场、矢量场)是为了保留它们的自身起源与物理意义.
[梯度]
grad![]() =(
=(![]() ,
,![]() ,
,![]() )=
)=![]() =
=![]() i+
i+![]() j+
j+![]() k
k
式中![]() =i
=i![]() +j
+j![]() +k
+k![]() 称为哈密顿算子,也称为耐普拉算子.grad
称为哈密顿算子,也称为耐普拉算子.grad![]() 有的书刊中记作del
有的书刊中记作del![]() .
.
grad![]() 的方向与过点(x,y,z)的等量面
的方向与过点(x,y,z)的等量面![]() =C的法线方向N重合,并指向
=C的法线方向N重合,并指向![]() 增加的一方,是函数
增加的一方,是函数![]() 变化率最大的方向,它的长度等于
变化率最大的方向,它的长度等于![]() .
.
梯度具有性质:
grad(![]()
![]() +
+![]() )=
)=![]() grad
grad![]() +
+![]() grad
grad![]() (
(![]() 、
、![]() 为常数)
为常数)
grad(![]()
![]() )=
)=![]() grad
grad![]() +
+![]() grad
grad![]()
gradF(![]() )=
)=![]()
[方向导数]
![]() =l·grad
=l·grad![]() =
=![]() cos
cos![]() +
+![]() cos
cos![]() +
+![]() cos
cos![]()
式中l=(cos![]() ,cos
,cos![]() ,cos
,cos![]() )为方向l的单位矢量,
)为方向l的单位矢量,![]() ,
,![]() ,
,![]() 为其方向角.
为其方向角.
方向导数为![]() 在方向l上的变化律,它等于梯度在方向l上的投影.
在方向l上的变化律,它等于梯度在方向l上的投影.
[散度]
divr=![]() +
+![]() +
+![]() =
=![]() ·r=div(X , Y , Z)
·r=div(X , Y , Z)
式中![]() 为哈密顿算子.
为哈密顿算子.
散度具有性质:
div(![]() a+
a+![]() b)=
b)=![]() diva+
diva+![]() divb (
divb (![]() 、
、![]() 为常数)
为常数)
div(![]() a)=
a)=![]() div a+a grad
div a+a grad![]()
div(a×b)=b·rot a-a·rotb
[旋度]
rotr=(![]() )i+(
)i+(![]() )j+(
)j+(![]() )k=
)k=![]() ×r=
×r=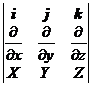
式中![]() 为哈密顿算子,旋度也称涡度,rot r有的书刊中记作curl r.
为哈密顿算子,旋度也称涡度,rot r有的书刊中记作curl r.
旋度具有性质:
rot(![]() a+
a+![]() b)=
b)=![]() rot a+
rot a+![]() rot b (
rot b (![]() 、
、![]() 为常数)
为常数)
rot(![]() a)=
a)=![]() rot a+a×grad
rot a+a×grad![]()
rot(a×b)=(b·![]() )a-(a·
)a-(a·![]() )b+(div b)a-(div a)b
)b+(div b)a-(div a)b
[梯度、散度、旋度混合运算] 运算grad作用到一个标量场![]() 产生矢量场grad
产生矢量场grad![]() ,运算div作用到一个矢量场 r产生标量场div r,运算rot作用到一个矢量场r产生新的矢量场
,运算div作用到一个矢量场 r产生标量场div r,运算rot作用到一个矢量场r产生新的矢量场
rot
r.这三种运算的混合运算公式如下:
div rot r=0
rot grad![]() =0
=0
div grad![]() =
=![]() +
+![]() +
+![]() =
=![]()
![]()
grad div r=![]() (
(![]() r)
r)
rot rot r=![]() ×(
×(![]() ×r)
×r)
div grad(![]()
![]() +
+![]() )=
)=![]() div grad
div grad![]() +
+![]() div grad
div grad![]() (
(![]() 、
、![]() 为常数)
为常数)
div grad(![]()
![]() )=
)=![]() div grad
div grad![]() +
+![]() div grad
div grad ![]() +2grad
+2grad![]() ·grad
·grad![]()
grad div r-rot rot r=![]() r
r
式中 ![]() 为哈密顿算子,
为哈密顿算子,![]() =
=![]() ·
·![]() =
=![]() 2为拉普拉斯算子.
2为拉普拉斯算子.
[势量场(守恒场)] 若矢量场r(x,y,z)是某一标函数![]() (x,y,z)的梯度,即
(x,y,z)的梯度,即
r=grad![]() 或 X=
或 X=![]() ,Y=
,Y=![]() ,Z=
,Z=![]()
则r称为势量场,标函数![]() 称为r的势函数.
称为r的势函数.
矢量场r为势量场的充分必要条件是:rot r=0,或
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]()
势函数计算公式
![]() (x,y,z)=
(x,y,z)=![]() (x0,y0,z0)+
(x0,y0,z0)+![]() +
+![]()
+![]()
[无散场(管形场)] 若矢量场r的散度为零,即div r=0,则r称为无散场.这时必存在一个无散场T,使r=rot T,对任意点M有
T=![]()
![]()
式中r为dV到M的距离,积分是对整个空间进行的.
[无旋场] 若矢量场r的旋度为零,即rot r=0,则r称为无旋场.势量场总是一个无旋场,这时必存在一个标函数![]() ,使r=grad
,使r=grad![]() ,而对任意点M有
,而对任意点M有
![]() =-
=-![]()
![]()
式中r为dV到M的距离,积分是对整个空间进行的.
二、
梯度、散度、旋度在不同坐标系中的表达式
1.单位矢量的变换
![]() [一般公式] 假定x=f(
[一般公式] 假定x=f(![]() ),y=g(
),y=g(![]() ),z=h(
),z=h(![]() )把(
)把(![]() )空间的一个区域 一对一地连续映射为(x,y,z)空间的一个区域D,并假定f,g,h都有连续偏导数,因为对应是一对一的,所以有
)空间的一个区域 一对一地连续映射为(x,y,z)空间的一个区域D,并假定f,g,h都有连续偏导数,因为对应是一对一的,所以有
![]()
![]() =
=![]() (x,y,z),
(x,y,z),![]()
再假定![]() 也有连续偏导数,则有
也有连续偏导数,则有
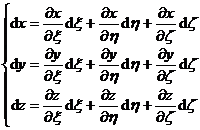
或逆变换
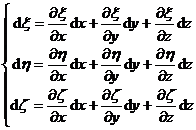
沿dx,dy,dz方向的单位矢量记作i,j,k,沿![]() 方向的单位矢量记作
方向的单位矢量记作![]() ,则有
,则有
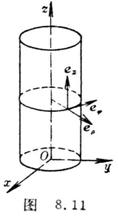
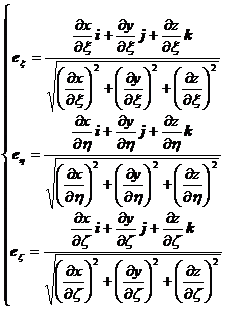
[圆柱面坐标系的单位矢量] 对于圆柱面坐标系(图8.11)
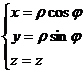
![]()
单位矢量为
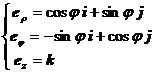
它们的偏导数为
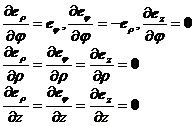
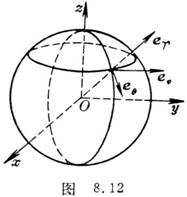
[球面坐标系的单位矢量] 对于球面坐标系(图8.12)
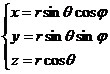
![]()
单位矢量为
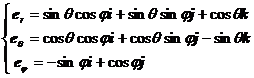
它们的偏导数为
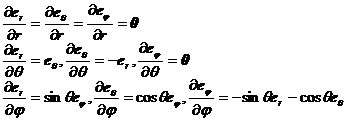
2.矢量的坐标变换
[一般公式] 一个由(x,y,z)坐标系所表达的矢量可以用(![]() )坐标系来表达:
)坐标系来表达:
![]() =(
=(![]() ,
,![]() y,
y,![]() z)=
z)=![]() i+
i+![]() y j+
y j+![]() z k=
z k=![]()
式中
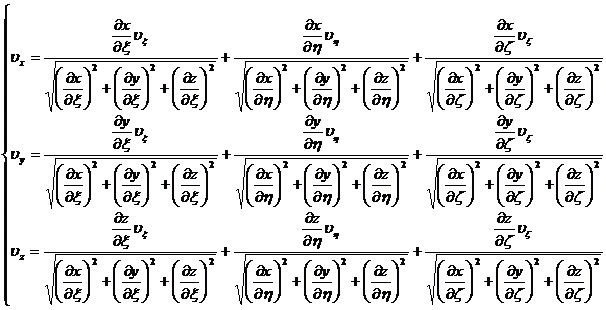
[圆柱面坐标系与直角坐标系的互换] 由圆柱面坐标系到直角坐标系的变换公式
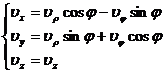
由直角坐标系到圆柱面坐标系的变换公式
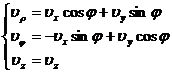
[球面坐标系与直角坐标系的互换] 由球面坐标系到直角坐标系的变换公式
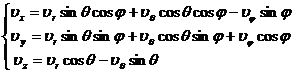
由直角坐标系到球面坐标系的变换公式
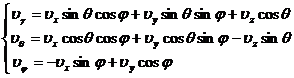
3.各种算子在不同坐标系中的表达式
设U=U(x,y,z)是一个标函数,V=V(x,y,z)是一个矢函数.
[在圆柱面坐标系中各种算子的表达式]
哈密顿算子 ![]() =
=![]() +
+![]() +
+![]()
梯 度 gradU= ![]() U=
U=![]() +
+![]() +
+![]()
散 度 divV= ![]() ·V=
·V=![]()
旋 度 rotV= ![]() ×V=
×V=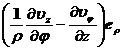 +
+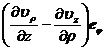 +
+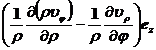
拉普拉斯算子 ![]() U=div gradU=
U=div gradU=![]()
[在球面坐标系中各种算子的表达式]
哈密顿算子 ![]() =
=![]() +
+![]() +
+![]()
梯 度 gradU= ![]() U=
U=![]() +
+![]() +
+![]()
散 度 div V=![]() ·V=
·V=![]()
旋 度 rotV= ![]() ×V=
×V=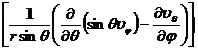
![]()
+![]()
![]()
+![]()
![]()
拉普拉斯算子 ![]() U=div gradU
U=div gradU
=![]()
三、
曲线积分、曲面积分与体积导数
[矢量的曲线积分及其计算公式] 矢量场r(r)沿曲线![]() 的曲线积分定义为
的曲线积分定义为
![]() r(r)·dr=
r(r)·dr=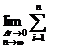 r(
r(![]() )·
)·![]() ri-1
ri-1
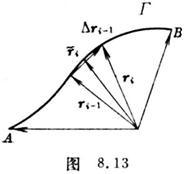 式中
式中![]() ri-1=ri-ri-1,右边极限与
ri-1=ri-ri-1,右边极限与![]() 的选择无关,曲线
的选择无关,曲线
![]() 由A到B(图8.13)
由A到B(图8.13)
若矢函数R(r)是连续的(就是它的三个分量是
连续函数), 曲线![]() 也是连续的, 且有连续转动的
也是连续的, 且有连续转动的
切线, 则曲线积分
![]()
存在.
若R(r)为一力场,则P=![]() 就等于把
就等于把
一质点沿着G 移动时力R所作的功.
矢量曲线积分的计算公式如下:
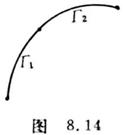
![]() =
=![]()
![]() =
=![]() +
+![]() (图8.14)
(图8.14)
![]() =-
=-![]()
![]() =
=![]() +
+![]()
![]() =k
=k![]() (k为常数)
(k为常数)
[矢量的环流] 如果G为一闭曲线,则沿曲线G 的曲线积分
![]() =
=![]()
称为矢量场R(r)沿闭曲线G 的环流.
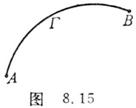 势量场沿任何闭曲线的环流都等于零.如果R(r)为一势量场,且它的势函数为
势量场沿任何闭曲线的环流都等于零.如果R(r)为一势量场,且它的势函数为![]() 时,则曲线积分
时,则曲线积分
![]() =
=![]() =
=![]() (B)-
(B)-![]() (A)
(A)
与连接A,B两点的路径无关,只依赖于A,B两点的
位置(图8.15).
[矢量的曲面积分] 设S为一曲面,令N=![]() 表示在曲面S上一点的法线单位矢量,V而dS=NdS表示面积矢量元素.又设
表示在曲面S上一点的法线单位矢量,V而dS=NdS表示面积矢量元素.又设![]() (r)=
(r)=![]() (x, y,z)是定义在曲面S上的连续标函数,R(r)=(X(x, y,z),Y(x, y,z), Z(x,
y,z))是定义在曲面S上的连续矢函数,则曲面积分有如下的三种形式:
(x, y,z)是定义在曲面S上的连续标函数,R(r)=(X(x, y,z),Y(x, y,z), Z(x,
y,z))是定义在曲面S上的连续矢函数,则曲面积分有如下的三种形式:
1![]() 标量场的通量(或流量)
标量场的通量(或流量)
![]() dS=
dS=![]() dydz i+
dydz i+![]() dzdx j+
dzdx j+![]() dxdy k
dxdy k
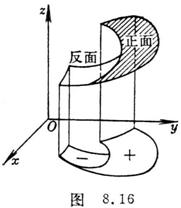
式中Syz,Szx,Sxy分别表示曲面S在Oyz平面,Ozx平面,
Oxy平面上的投影.Sxy的正负号规定如下:当从z轴正方
向看去时,看到的是曲面S的正面,认为Sxy为正,如果
看到的是曲面的反面,则认为Sxy为负(图8.16).
2![]() 矢量场的标通量
矢量场的标通量
![]() R·dS=
R·dS=![]() Xdydz+
Xdydz+![]() Ydzdx+
Ydzdx+![]() Zdxdy
Zdxdy
式中Syz等的意义同1![]() .
.
3![]() 矢量场的矢通量
矢量场的矢通量
![]() R×dS=
R×dS=![]() (Zj-Yk)dydz+
(Zj-Yk)dydz+![]() (Xk-Zi)dzdx+
(Xk-Zi)dzdx+![]() (Yi-Xj)dxdy
(Yi-Xj)dxdy
式中Syz等的意义同1![]() .
.
[矢量的体积导数] 如果S是包围体积V的闭曲面,并包含点r,则沿闭曲面S的曲面积分(![]()
![]() dS,
dS, ![]() R·dS,
R·dS,
![]() R×dS)与体积V之比,当V趋于零时(即它的直径
R×dS)与体积V之比,当V趋于零时(即它的直径![]() 0)的极限称为标量场
0)的极限称为标量场![]() (或矢量场R)在点r处的体积导数(或空间导数).
(或矢量场R)在点r处的体积导数(或空间导数).
1![]() 标量场
标量场![]() 的体积导数就是它的梯度:
的体积导数就是它的梯度:
grad![]() =
=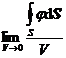
2![]() 矢量场R的体积导数之一是它的散度:
矢量场R的体积导数之一是它的散度:
div
R=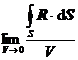
3![]() 矢量场R的另一个体积导数是它的旋度:
矢量场R的另一个体积导数是它的旋度:
rot
R=-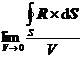
四、
矢量的积分定理
[高斯公式]
![]() RdV=
RdV=![]() R·dS=
R·dS=![]() R·NdS
R·NdS
即
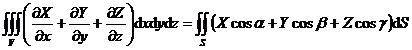
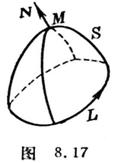 式中S为空间区域V的边界曲面,N=
式中S为空间区域V的边界曲面,N=![]() 为
为
在S上一点的法线单位矢量,R(r)=(X(x, y,z),Y(x, y,z),Z(x, y,z))
在V+S上有连续偏导数.
[斯托克斯公式]
![]() rot R·dS=
rot R·dS=![]() rot R·NdS=
rot R·NdS=![]() R·dr
R·dr
即
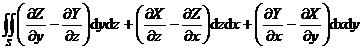
= 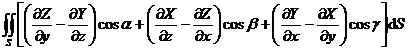
= ![]()
式中S为一定曲面的一侧,L为曲面S的闭边界曲线(L的正向与N构成右手系).S的每点有切面,其方向连续地依赖于曲面上的点,而边界曲线L上的每点都有切线(图8.17). R(r)=(X(x,
y,z),Y(x,
y,z),Z(x,
y,z))在曲面的所有点单值,并在与S足够靠近的点处有连续偏导数.
[格林公式]
![]() ·dS=
·dS=![]()
![]() ·dS=
·dS=![]()
式中S为空间区域V的边界曲面,![]() 为两个标函数,在S上具有连续偏导数,且在V上具有二阶连续偏导数,
为两个标函数,在S上具有连续偏导数,且在V上具有二阶连续偏导数,![]() 为拉普拉斯算子,特别
为拉普拉斯算子,特别
![]() ·dS=
·dS=![]()
即