二、解析函数
一般地,复数函数ω=f(z)可以写成
这样,对于一般的复变函数的讨论就等价于对两个双变量的实变函数的讨论.但是,在生产实践和科学实验中,常常遇到的是一类比较特殊的复变函数——解析函数.对于这一类函数,去研究复变函数f(z)本身比拆开来研究两个实变函数u(x,y)和v(x,y)更方便,得到的结论更简捷完整,便于应用.
1、解析函数的定义与柯西-黎曼方程
[解析函数与柯西-黎曼方程] 如果复变函数f(z)在点z=z0的一个充分小领域*内点点可微,就称这个函数在点z0是解析的;如果函数f(z)在一个区域Σ内点点可微就称它在区域Σ内是解析的(正则,全纯).
如果定义在区域Σ内的函数
![]()
在Σ内解析,那末u(x,y)和v(x,y)在Σ内满足下面的柯西-黎曼方程
![]()
反过来,如果u(x,y),v(x,y)在Σ内满足上面的条件,并且可微,那末f(z)在Σ内解析.这时,解析函数f(z)的导数可以表示成下面四种形式之一:
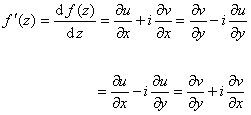
[调和函数] 在区域Σ内存在二阶连续偏导数的实变函数u(x,y),如果在Σ内满足拉普拉斯方程
![]()
那末称函数u=u(x,y)是Σ内的调和函数.
区域Σ内的解析函数f(z)的实部和虚部都是调和函数.
[形式导数] 将

或
![]()
看作变量替换而引进形式导数
如果f(x,y)是实变数x,y的有连续偏导数的函数,那末
这样一来,柯西-黎曼方程可写成
拉普拉斯方程可写成
极坐标![]() 中的柯西-黎曼方程可写成
中的柯西-黎曼方程可写成