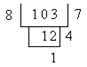The first chapter algebra, trigonometry formulas and elementary functions
Here the collection and collation of elementary algebra ( see Chapter III of algebraic equations part ) , some commonly used formulas plane and spherical trigonometry triangle, but also introduces some common elementary functions ( a real independent variable ) the nature and simple graphics, so this chapter basically includes the main content of secondary school algebra and trigonometry .
§ 1 algebraic formulas
First, the number of expansion, classification and basic arithmetic rules
1 . number of expansion and classification
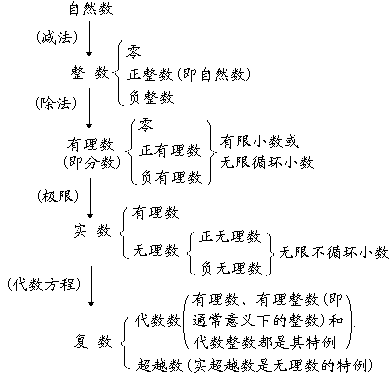
2 . real number four arithmetic rules
[ Modified regulations are ] the same number two numbers together, absolute values, symbols and addend same; different number two numbers together, the absolute value subtraction ( large decrease ) , and the absolute value of a big plus sign Number of same; any real number and zero sum, equal to the real number itself . subtraction is the inverse operation of addition, subtraction of two numbers as long as the subtrahend into opposite number with its symbol, you can rule by the addition operation .
[ multiplication and division regulations are ] the number is multiplied with the number two, the absolute value is multiplied by the sign is positive; different numbers multiplying two numbers, the absolute value is multiplied by a negative sign; any number multiplied by zero is zero; any number with a phase Take equal to its own . division is the inverse of multiplication, division number with number two, the absolute value of the division, the sign is positive; different number divided by two numbers, the absolute value of the division, the sign is negative; any number divided by an equal its own; zero divided by any number is not zero is equal to zero; zero divisor can not do .
[ four mixed computing rules ] to multiplication and division, addition and subtraction; within the first brackets, outside the parentheses .
3 Number of three basic laws of arithmetic
[ commutative ]![]()
![]()
[ associative ]![]()
![]()
[ distributive ]![]()
4. involution and prescribing
[ power of ] N number of a multiplying
![]()
n months
Called a a n times ( multiply ) party, also known as a the n -th power . a known power base, N is called the exponent .
Obtained directly from a power symbol symbol rule multiplication rule: Any power of positive numbers is positive; negative dual power of a positive number; negative odd power of negative; any power of zero is zero .
Provision does not equal zero zero power equal to the number of one , namely a 0 = 1 , a 1 0 .
[ square root ] If a 2 = b , then a called b of the square root, denoted by ![]() , the square root of the square root operation is called . general approach illustrated by the square root of the examples below .
, the square root of the square root operation is called . general approach illustrated by the square root of the examples below .
Cases seeking 316.4841 square root .
Solution The first step , the first number is the square root of the decimal point to the left and right position every two comma "," segments, such as the number 316.4841 segmented into 3,16.48,41 . second step, find the first Manufacturers of digital the initial period, so that the beginning of the first stage does not exceed the square's number, and the beginning of the provider plus a square of the first segment is greater than the number, this number is the first paragraph of Example 3 , provided for the beginning of 1 , because the 1 2 = 1 <3 , and (1 + 1) 2 = 4> 3 . third step, by subtracting the square of the first stage's digital First and second digital moved down, the remainder consisting of the first, in the present Examples of the first remainder 216 . fourth step, try to find providers, so (20 ' early commercial + test providers ) ' test provider does not exceed the first remainder, while [20 ' early commercial + ( test provider +1 )] ' ( test provider +1) is greater than the first remainder . fifth step, the first remainder minus (20 ' early commercial + test providers ) ' test providers, and move under the third paragraph numbers, the composition of the first Second remainder, in this case the test provider for seven , the second remainder is 2748 . shall thereafter continue to do so until all of the sections of the shift, if the last remainder is zero, the root operation ended . If the remainder is never zero, you can only take a certain precision approximation . sixth step, set the decimal point position, the position of the square root of the decimal point should be aligned with the square root of the number of decimal point position . this example formula is as follows:

[ Open Cube ] If a 3 = b , then a called b of the cube root, denoted by ![]() , find the cube root of the operation called open cube .
, find the cube root of the operation called open cube .
Square root and cube root of a number can be found from the "square root" and the "cube root table" .
5 real binary system
[ binary system of base and digital ] any positive number can be expressed as a finite or infinite decimal decimal usual sense, the position of each digit numeric value and where relevant, any location numbers to the right of the decimal point when its value expanded 10 -fold, when the decimal point to the left one when its value is reduced 10 -fold . example
![]()
Generally, either a positive number a can be expressed as
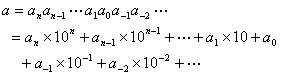
This is the 10 binary numbers, denoted a (10) , the number 10 is called binary system group wherein a i in {0,1,2, L , 9} in the value called 10 -adic number, Obviously there is no reason to say that the basic binary system can not take another number . now take q is any greater than a positive integer binary system as the base, so they get q into the number indicates
![]() (1)
(1)
Wherein the number a i in {0,1,2, L , q -1} of values, a N a N -1 L a 1 a 0 is called q -adic a ( q ) is the integer part, referred to as [ a ( q ) ];
a -1 a -2 L is called a ( q ) the fractional part, denoted by { a ( q ) } . usual binary system, in addition to 10 decimal, there are two binary, 8 hex, 16 hex, etc. , it follows
2 binary 0, 1
8 binary 0, 1, 2, 3, 4, 5, 6, 7
16 hexadecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
![]()
[ 2 , 8 , 16 hex addition and multiplication tables ]
|
2 binary adder table |
|
Two decimal multiplication table |
||||
|
+ |
0 |
1 |
|
|
0 |
1 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
1 |
1 |
10 |
|
1 |
0 |
1 |
8 binary adder table
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
|
1 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
10 |
|
2 |
02 |
03 |
04 |
05 |
06 |
07 |
10 |
11 |
|
3 |
03 |
04 |
05 |
06 |
07 |
10 |
11 |
12 |
|
4 |
04 |
05 |
06 |
07 |
10 |
11 |
12 |
13 |
|
5 |
05 |
06 |
07 |
10 |
11 |
12 |
13 |
14 |
|
6 |
06 |
07 |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
07 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
8 decimal multiplication table
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
1 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
|
2 |
00 |
02 |
04 |
06 |
10 |
12 |
14 |
16 |
|
3 |
00 |
03 |
06 |
11 |
14 |
17 |
Twenty two |
25 |
|
4 |
00 |
04 |
10 |
14 |
20 |
Twenty four |
30 |
34 |
|
5 |
00 |
05 |
12 |
17 |
Twenty four |
31 |
36 |
43 |
|
6 |
00 |
06 |
14 |
Twenty two |
30 |
36 |
44 |
52 |
|
7 |
00 |
07 |
16 |
25 |
34 |
43 |
52 |
61 |
16 hex Addition Table
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
0 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
|
1 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
0 |
|
|
|
|
10 |
|
2 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
|
3 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
|
4 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
16 hex Addition Table
|
5 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
|
6 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
8 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
9 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
16 hexadecimal multiplication table
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
0 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
1 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
|
2 |
00 |
02 |
04 |
06 |
08 |
|
|
|
10 |
12 |
14 |
16 |
18 |
|
|
|
|
3 |
00 |
03 |
06 |
09 |
|
|
12 |
15 |
18 |
|
|
Twenty one |
Twenty four |
27 |
|
|
|
4 |
00 |
04 |
08 |
|
10 |
14 |
18 |
|
20 |
Twenty four |
28 |
|
30 |
34 |
38 |
|
|
5 |
00 |
05 |
|
|
14 |
19 |
|
Twenty three |
28 |
|
32 |
37 |
|
41 |
46 |
|
|
6 |
00 |
06 |
|
12 |
18 |
|
Twenty four |
|
30 |
36 |
|
42 |
48 |
|
54 |
|
|
7 |
00 |
07 |
|
15 |
|
Twenty three |
|
31 |
38 |
|
46 |
|
54 |
|
62 |
69 |
|
8 |
00 |
08 |
10 |
18 |
20 |
28 |
30 |
38 |
40 |
48 |
50 |
58 |
60 |
68 |
70 |
78 |
|
9 |
00 |
09 |
12 |
|
Twenty four |
|
36 |
|
48 |
51 |
|
63 |
|
75 |
|
87 |
|
|
00 |
|
14 |
|
28 |
32 |
|
46 |
50 |
|
64 |
|
78 |
82 |
|
96 |
|
|
00 |
|
16 |
Twenty one |
|
37 |
42 |
|
58 |
63 |
|
79 |
84 |
|
|
|
|
|
00 |
|
18 |
Twenty four |
30 |
|
48 |
54 |
60 |
|
78 |
84 |
90 |
|
|
|
|
|
00 |
|
|
27 |
34 |
41 |
|
|
68 |
75 |
82 |
|
|
|
|
|
|
|
00 |
|
|
|
38 |
46 |
54 |
62 |
70 |
|
|
|
|
|
|
|
|
|
00 |
|
|
|
|
|
|
69 |
78 |
87 |
96 |
|
|
|
|
|
[ 8-2 , 16-2 digital conversion table ]
|
8 binary numbers |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Two binary numbers |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
16 into the number of |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Two binary numbers |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
16 into the number of |
8 |
9 |
|
|
|
|
|
|
|
Two binary numbers |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
[ various binary system of mutual conversion ]
1 ° q Õ 10 conversion is generally applicable to the 10 -adic four rules of arithmetic, according to the formula (1) may be the q -adic a ( q ) is converted to 10 binary numbers represented . e.g.
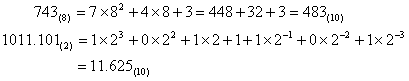
2 ° 10 Õ q converted into integer and fractional must be part of the conversion .
For integer part of its steps are:
(1) with q removal of [ a (10) ] , the quotient and remainder .
(2) Write down the remainder as q enter the last digit number .
(3) Replace with suppliers [ a (10) ] position to repeat (1) and (2) a two-step, until the quotient is equal to zero .
For the fractional part of its steps are:
(1) with q to multiply { a (10) } .
(2) the product of the integer part of a note as q into the fractional part of the first digit of the number .
(3) the product of the fractional portion is replaced with { a (10) } of position and repeat (1) and (2) steps, until the product of the integer has been changed, or until the desired number of bits is reached . e.g.:
103.118 (10) = 147.074324 L (8)
|
The integer part of the grass-type |
Fractional portion of the grass-type |
|
|
|
3 ° P Õ q converter usually comprises the following steps: a ( P ) Õ a (10) Õ a ( q ) . if P , q is the same number s of different powers, comprises the following steps: a ( P ) Õ a ( s ) Õ a ( q ) . example, eight into the number 127.653 (8) converted into 16 binary numbers, since 8 = 2 3 , 16 = 2 4 , so s = 2 , the steps are: First, the eight into Each digit number according to the 8-2 conversion table into two binary numbers ( three group )
127.653 (8) = 001 010 111.110 101 011 (2)
Then the two numbers from all the numbers into the decimal point onwards ( left and right ) of each grouping a set of four, from 16-2 individually write down the corresponding conversion table 16 into the number of digits, namely
![]()
Second, the complex
1 concept plural
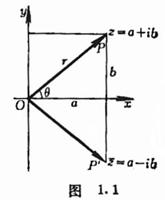
[ · real and imaginary parts of the mold and the radiation angle and a complex conjugate of ] the complex z is typically expressed as z = a + ib , which ![]() is called the imaginary unit, a and b are real numbers, called z real part and the imaginary part , referred to as a = Re z , b = Im z .
is called the imaginary unit, a and b are real numbers, called z real part and the imaginary part , referred to as a = Re z , b = Im z .
Two complex only when the real and imaginary parts are equal equal .
![]() Called the complex z die .
Called the complex z die .
![]() Called the complex z spoke angle, so there is an infinite number of complex convergence angle, but one called Lord spoke angle, denoted by Arg z , which satisfies
Called the complex z spoke angle, so there is an infinite number of complex convergence angle, but one called Lord spoke angle, denoted by Arg z , which satisfies
0 ≤ Arg z <2 P
And a Arg z = Arg z +2 k P ( k = 0, ± 1, ± 2, L )
![]() With the
With the ![]() complex conjugate of each other .
complex conjugate of each other .
[ imaginary unit of involution ]
![]()
![]()
|
|
2 . Complex notation
[ coordinate notation ] complex z = a + ib with Cartesian coordinates ( a , b ) establish correspondence ( Figure 1.1).
[ Vector notation ] The a , b considered a vector ![]() in the x -axis and y -axis projection of the vector
in the x -axis and y -axis projection of the vector ![]() ( Figure 1.1) can be expressed the complex z = a + ib , and P the point on the x -axis point of symmetry referred to as
( Figure 1.1) can be expressed the complex z = a + ib , and P the point on the x -axis point of symmetry referred to as ![]() vector
vector ![]() represents the complex conjugate
represents the complex conjugate ![]() .
.
[ triangle notation ] ![]()
![]()
[ exponential notation ] ![]()
3 . Complex arithmetic
[ algebraic computation ]
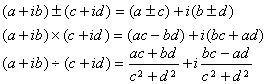
[ Triangle op ] set
![]()
Then ![]()
![]()
![]()
When r 1 = 1 when, too ![]() , this formula is called Germany · Morpho formula .
, this formula is called Germany · Morpho formula .
![]()
[ exponential operator ] set
![]()
Then ![]()
![]()
Third, the number of columns and simple progression
1 . Concept Series and the
Arranged in accordance with a rule number one column
a 1 , a 2 , a 3 , L , a N , L
Called the number of columns, denoted by { a N }. If the number of the number of columns and link up with:
a 1 + a 2 + a 3 + L + a N + L
It is called the series, denoted by ![]() . a N called the number of columns or the corresponding series of general term (or referred to in general terms) .
. a N called the number of columns or the corresponding series of general term (or referred to in general terms) .
2 . Arithmetic sequence and arithmetic (arithmetic) progression
a 1 , a 1 + d , a 1 +2 d , a 1 +3 d , L ( d is a constant )
Called tolerance d arithmetic sequence . arithmetic sequence with the corresponding series called arithmetic progression, also known as the arithmetic progression .
General term formula ![]()
Before n items and ![]()
Items in arithmetic ![]()
3 . Geometric sequence with geometric (geometric) series
a 1 , a 1 q , a 1 q 2 , a 1 q 3 , L ( q is a constant )
Called the common ratio of q geometric columns . geometric sequence with the corresponding series called geometric progression, also known as geometric progression .
General term formula ![]()
Before n items and ![]()
Geometric mean ![]()
Infinite decreasing geometric progression and ![]()
4 . Arithmetic - geometric series
![]() ≥ 1)
≥ 1)
![]()
5 . Harmonic Series
1 O if ![]() for arithmetic progression, then a + b + c + L called the harmonic series . reconcile the entry for
for arithmetic progression, then a + b + c + L called the harmonic series . reconcile the entry for
![]()
2 O set A , G , H , respectively, for a term of two numbers in arithmetic, geometric mean and reconcile the item,
AH = G 2
6 . Higher-order arithmetic progression
There is a number of columns
a 1 , a 2 , L , a N , L (1)
* If successively subtracting the latter from its one, then get the number of columns of the original (1) constituting the difference between the first number of columns
a 2 - a 1 , a 3 - a 2 , L , a N - a N-1 , L (2)
Then successively the (2) subtracting one of the previous one, and to give the number of columns (1) the difference between the number of columns in the second configuration . and so on:
a 1 a 2 a 3 a 4 L
The first difference d 1 = D a 1 D a 2 D a 3 L
The second difference d 2 = D 2 a 1 D 2 a 2 L
The third difference d 3 = D 3 a 1 L
LL
Where ![]()
If you do a r times, the number of columns (1) Each section r times poor are equal, then the poor are equal to zero after each time, called the number of columns (1) of r -order arithmetic sequence . with such number of columns corresponding series called for r -order arithmetic progression . an order arithmetic progression is the usual arithmetic progression .
Set (1) is a r -order arithmetic sequence, and let d 1 is (1) the difference between the form of the first series of the first term, d 2 is (1) a second time difference constitutes the first item number column, L , d r of (1) the first r columns constituting the difference between the first line item, then there
General term formula ( N > r )
![]()
Before n items and
![]()
7 . Part and certain series
![]()
![]()
![]()
![]()
![]()
![]()
![]()
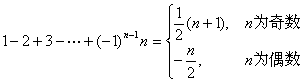
![]()
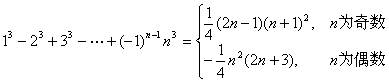
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
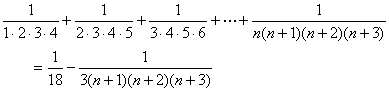
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
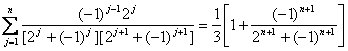
![]()
Fourth, multiplication and factorization formula
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Five, fractional
1. fractional arithmetic
![]()
![]()
![]()
![]()
![]()
![]()
2. partial fraction
Any irreducible Fraction ( numerator and denominator have no common factor, the number of molecules times lower than the denominator ) can be decomposed uniquely shaped like ![]() or
or 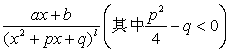 fraction of a basic truth and its operation is called partial fraction expansion . If it is false Fractional ( molecular number is not less than the denominator number ) , should be translated into Zhengshi fraction of the true and then carried on Franctions partial fraction expansion . each partial fraction coefficients can be determined by the method of undetermined coefficients . Below are several different points briefing .
fraction of a basic truth and its operation is called partial fraction expansion . If it is false Fractional ( molecular number is not less than the denominator number ) , should be translated into Zhengshi fraction of the true and then carried on Franctions partial fraction expansion . each partial fraction coefficients can be determined by the method of undetermined coefficients . Below are several different points briefing .
Set ![]()
![]()
[ linear factor Repeat ]
1 O ![]()
Where N ( x ) the maximum number of r ≤ m -1 ; A 0 , A 1 , L , A m -1 for undetermined constants determined by the following formula:
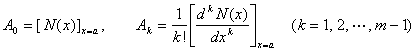
2 O ![]()
Where A 0 , A 1 , L , A m is determined constant, determined by the following formula:
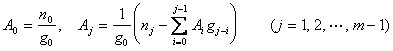
![]() ≤ s -1
≤ s -1
Coefficients f J and m concerned, is determined by the following table:
|
m |
f J ( J = 0, 1, 2, L , k ; k ≤ s -1) |
|
1 |
|
|
2 |
|
|
3 |
|
|
M |
LLLLLLLL |
|
m |
|
Case ![]()
Solutions calculated according to the above formula
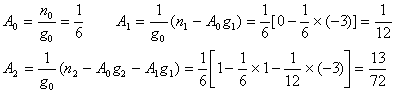
In this case m = 3 ,
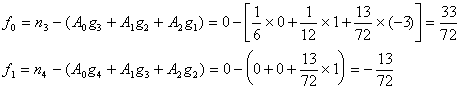
So get
![]()
3 O ![]()
For the transformation y = x - a , then N ( x ) = N 1 ( y ), G ( x ) = G 1 ( y ), the above equation becomes
![]()
The above-mentioned 1 O , 2 O method for determining the A 0 , A 1 , L , A m -1 and F 1 ( y ) , then y = x - a generation back . following formula can be used to determine the coefficients A 0 , A 1 , L , A m -1 :

[ linear factor does not repeat ]
1 O ![]()
Where N ( x ) the maximum number of r ≤ 2 , a 1 b 1 c ; A , B , C as determined constant, determined by the following formula:
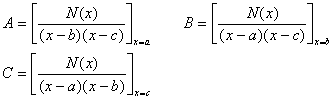
2 O
![]()
Where the polynomial F ( x ) the maximum number k ≤ s-1 ; A , B is a constant determined by the following formula:
![]()
A , B determined, then the same polynomial equation on both sides must be equal to the coefficient rules to determine F ( x ) of the coefficients .
Case ![]()
Solutions to be considered according to the above formula
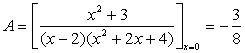
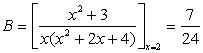
The A , B substituting the original style, the common denominator and finishing too
![]()
Compare both sides of the equation have the same coefficient times
![]()
So there
![]()
[ higher-order factor ]
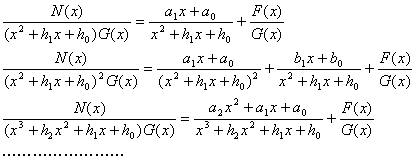
[ general method for calculating the coefficient of ]
![]()
1 O on both sides of the equation is multiplied by D ( x ) into Zhengshi, the press x combined with the power, and then list the equations the unknown coefficients derived solved .
2 O on both sides of the equation multiplied by D ( x ) into Zhengshi, then the x value with a simple ( e.g. x = 0, 1, -1 , etc ) is substituted, then the unknown coefficients listed equations, the solution of obtained .
Six, the proportion of
1 O if ![]() ( or written as a : b = c : d ) , a , b , c , d is not zero,
( or written as a : b = c : d ) , a , b , c , d is not zero,
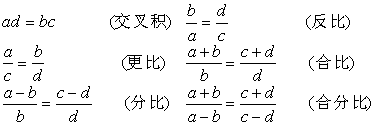
2 O if ![]() , then
, then
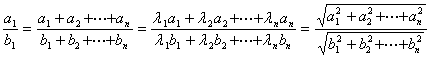
Where L i ( i = 1, 2, L , N ) for a group of an arbitrary constant, b i ( i = 1, 2, L , N ) is not equal to zero .
3 O if y and x is proportional to ( denoted by y mu x ) , then
![]()
If y and x is inversely proportional ![]() , then
, then
![]()
If y and x proportional, y and z are proportional ( i.e., y mu x , y mu z ) , the x and z is proportional to the
![]()
And y and xz proportional, ie
![]()
Seven, radical
1. radical concept
[ root and radical ] number a of the n -th root refers to seek a number of its n -th power is exactly equal to a . a the n -th root denoted by ![]() ( N is greater than a natural number ). as algebra,
( N is greater than a natural number ). as algebra, ![]() called radical . N called the root index, a foundation called the number . within the range of real numbers, negative numbers can not be opened even th power, even power of a positive open with two root, the same absolute value, the opposite sign .
called radical . N called the root index, a foundation called the number . within the range of real numbers, negative numbers can not be opened even th power, even power of a positive open with two root, the same absolute value, the opposite sign .
[ arithmetic root ] positive square root of the root is called arithmetic . arithmetic root of zero is zero provisions .
[ basic properties ] from the definition of root, there is
![]()
2. radical operation
[ square root of the product ] is equal to the square root of the product of each factor with th root of the product; turn, is equal to the product of the same th root of the product of the same th root, namely
![]() ≥ 0, b ≥ 0)
≥ 0, b ≥ 0)
[ Fraction root ] fractions equal to the square root of the numerator and denominator with th root division, namely
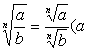 ≥ 0, b > 0)
≥ 0, b > 0)
[ Radical involution ] ![]() ≥ 0)
≥ 0)
[ radical simplification ]
![]() ≥ 0)
≥ 0)
![]()
![]()
![]() ≥ 0, d ≥ 0)
≥ 0, d ≥ 0)
![]()
![]() ≥ 0, d ≥ 0)
≥ 0, d ≥ 0)
[ similar radical and addition and subtraction ] root index and the foundation have the same number of similar radical radical known only available to be consolidated with similar radical addition and subtraction .
Eight, inequality
1 simple inequality
1 O if a > b , then

2 O
if ![]() and b , d same number, then
and b , d same number, then
![]()
2. related to absolute inequality
1 O If a , b , L , k is an arbitrary complex number, then
![]() ≤
≤![]()
![]() ≤
≤![]()
![]()
2 O , if a , b is an arbitrary complex number, then
![]() ≤
≤ ![]() ≤
≤![]()
3 O
if ![]() ≤
≤ ![]() , the
, the
![]() ≤
≤ ![]() ≤
≤ ![]() particularly
particularly ![]() ≤
≤ ![]() ≤
≤![]()
4 O
if ![]() ≥
≥ ![]() , then
, then
![]() Or
Or![]()
3. related trigonometric, exponential, logarithmic function of inequality
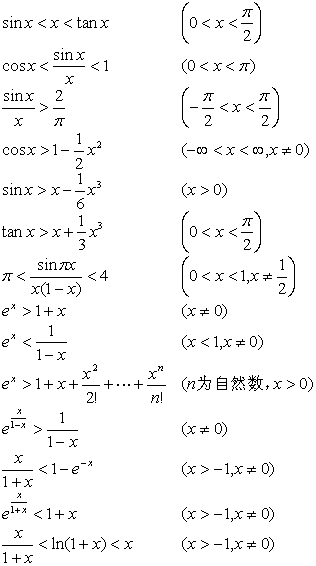
Take particular ![]() , there
, there
![]()
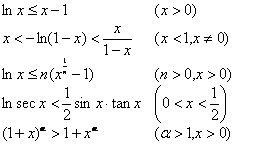
( The following kinds of variable z is a complex number )
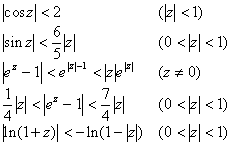
4. certain important inequality
[ arithmetic mean and the geometric mean inequality ]
1 O arithmetic average of the absolute value of a few number does not exceed the number of rms, namely
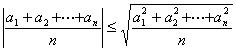
Equals only when ![]() true .
true .
2 O provided a 1 , a 2 , L , a N are positive, their geometric mean is not more than the arithmetic mean value, i.e.,
![]()
Equals only when ![]() true .
true .
3 O
of n positive number a 1 , a 2 ,
L , a N -weighted average ![]() , with
, with
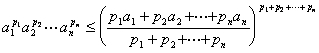
Equals only if a 1 = a 2 = L = a N true .
4 O
located a 1 , a 2 ,
L , a N is a positive number, and ![]() , if there
, if there
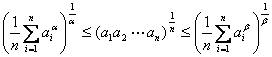
[ Cauchy inequality ] set a i , b i ( i = 1, 2, L , N ) is an arbitrary real number,
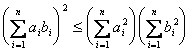
Only if the equal sign ![]() are true . this inequality indicating that a corner ( takes real value ) is always less than the cosine of a , or the product of the second product is less than the second vector within the vector length .
are true . this inequality indicating that a corner ( takes real value ) is always less than the cosine of a , or the product of the second product is less than the second vector within the vector length .
[ Herder inequality ]
1 O located a i , b i , L , L i ( i = 1, 2, L , N ) is a positive number, and a , b , L , L is a positive number, and a + b + L + L = 1 , then
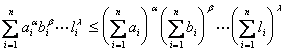
Equals only when ![]() true .
true .
2 O
provided a i , b i ( i = 1, 2, L , N ) is a positive number, and k > 0, k 1 1, ![]() and k conjugate, i.e.
and k conjugate, i.e. ![]() , or
, or ![]() , if
, if

Equals only when ![]() true .
true .
[ Minkowski inequality ] set a i , b i > 0 ( i = 1, 2, L , N ) , and r > 0, r 1 1, then

Equals only when ![]() true . When r = 2 , this inequality is also known as the triangle inequality, it shows two sides of a triangle is greater than the third side .
true . When r = 2 , this inequality is also known as the triangle inequality, it shows two sides of a triangle is greater than the third side .
[ Chebyshev inequality ] established a i > 0, b i > 0 ( i = 1, 2, L , N ). If a 1 £ a 2 £ L £ a N , and b 1 £ b 2 £ L £ b N , or a 1 3 a 2 3 L 3 a N , and b 1 3 b 2 3 L 3 b N , then
![]()
If a 1 £ a 2 £ L £ a N and b 1 3 b 2 3 L 3 b N , then
![]()
[ Zhan Health Inequality ] established a i > 0 ( i = 1, 2, L , N ) , and 0 < r £ s , then

[ Bernoulli inequality ] established a > 1 , a natural number N > 1 , then
![]()
Special orders ![]() , then
, then
![]()
5. quadratic inequalities Solution
![]() The solution ( set
The solution ( set ![]() )
)
|
|
D > 0 |
D = 0 |
D <0 |
|
a > 0 |
|
|
|
|
a <0 |
|
No solution |
No solution |
Nine, factorial, permutations and combinations
A. factorial
[ definition of factorial ] set n is a natural number, then
![]()
Called n factorial . and provides 0! = 1 and define
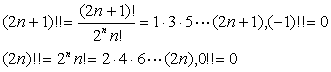
[ Stirling formula ]
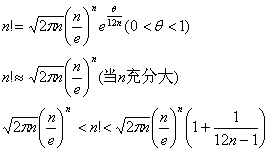
[ factorial limited and formulas ]

2. arrangement
[ optional arrangement ] from n distinct elements, each removing k a ( k £ N ) of different elements, arranged according to a certain order, called the election arrangement . their arrangement species for
![]()
[ full array ] from n distinct elements, each removing n distinct elements, arranged according to a certain order, called the whole arrangement . their arrangement species for
![]()
[ Duplicate arrangement ] from n distinct elements, each removing k elements ( k £ N ) , allowing repeated this arrangement is called duplicate arrangement . their arrangement species for
![]()
[ not the full array of different elements ] If the n elements, there are N 1 are the same elements, there are N 2 elements identical to each other, L , there are N m -th element are the same ( N 1 + N 2 + L + N m = N ) , then this n full array elements called full array countless different elements . their arrangement species for
![]()
[ ring arrangement ] from n distinct elements, each removing k elements, only by the relative position between the elements and end to end to form a circle, regardless, this arrangement method called cyclic arrangement . their arrangement species number
![]()
![]()
3. combination
[ usually a combination of sense ] from n distinct elements, each removing k distinct elements, regardless of the order combined into one group, called the combination . their portfolio species for
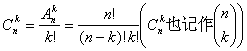
And regulations ![]() .
.
[ multiple combinations ] to n distinct elements into m groups, first i group N i distinct elements, namely ![]() , the number of species of this group is
, the number of species of this group is
![]()
Combination of common sense is a special case .
[ duplicate combinations ] from n different elements, each removal k elements, allowing repeated, regardless of the sequence are combined into a group, this combination is known to have a combination of repeating, the combination of species
![]()
[ combination formula ]




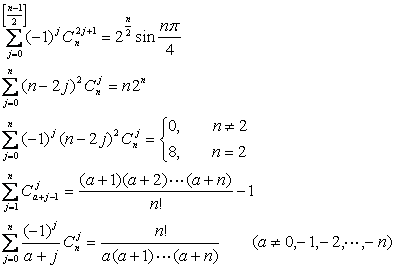
![]()
X. Triangle Theorem and polynomial
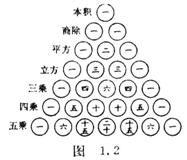
[ binomial theorem ]
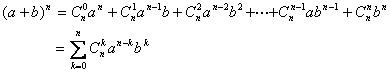
Wherein n is a positive integer ![]() called the two coefficients .
called the two coefficients .
|
|
[ Triangle ] of the Southern Song Dynasty mathematician Yang Hui in his book "Explanation IX algorithm" ( 1261 year ) recorded in the study about the two coefficients . the binomial theorem, when n were taken 0, 1, 2 , 3, 4, 5, 6 , the second coefficient expressed in Figure 1.2 , the so-called "Triangle" . Frenchman Pascal have similar results ( 1650 years ) , so foreign books referred to as "Pascal's triangle", but nearly four hundred years later than Pascal .
[ polynomial theorem ]
![]() And wherein each of the array ( P , q , L , s ) corresponds to one, the array satisfies 0 £ P £ N , 0 £ q £ N , L , 0 £ s £ N , P + q + L + s = N ,
S is the summation for all such arrays .
And wherein each of the array ( P , q , L , s ) corresponds to one, the array satisfies 0 £ P £ N , 0 £ q £ N , L , 0 £ s £ N , P + q + L + s = N ,
S is the summation for all such arrays .
XI, the principle of mathematical induction and drawers
[ mathematical induction ] to contain integer n formulas, that is, from a pair of integers from behind all integers n have established formulas, and sometimes can be used to prove mathematical induction . following steps:
1 O verification n takes the first value N 0 time ( e.g. N 0 = 0 , 1 , or 2 , etc. ) equation holds .
2 O is assumed that when N = k when the formula was established, to verify when N = k +1 is also true when the formula .
Because when the formula N = N 0 are true, so that the 2 O shows that, when N = N 0 +1 is also true when the formula; then by 2 O shows that, when N = N 0 + 1 + 1 = N 0 +2 when the formula also set up, continue to push down so we can see, for all greater than N 0 integer n formulas are established .
[ drawer principle ] N +1 an object into n a drawer, at least one drawer with two or more objects, this principle is called the drawer principle, it proves the existence theorem when certain useful . drawer principle points or less three forms:
1 O N +1 elements into n groups, there must be a group that contains at least two elements .
2 O m elements divided into n groups ( m > N is a positive integer ) , there must be a group containing at least ![]() one element ([ x ] represents x integer part ) .
one element ([ x ] represents x integer part ) .
3 O infinite number of elements into a finite group, there must be a group containing an infinite number of elements .