§ 4 Taylor series, Laurent series, residue theorem
1. Taylor series and Laurent series
1. Taylor series
[ Taylor series expansion theorem ] If the function is analyzed in the circle ( ), then the Taylor series can be expanded in the circle![]()
![]()
![]()
![]()
![]()
in the formula
![]()
where is the circle with the center of the circle and the radius of ( ) . This expansion is unique .![]()
![]()
![]()
![]()
The Taylor series expansion table of the complex variable function is similar to the power series expansion table of the real variable function (Chapter 5, § 3 , 9), as long as the real variables are replaced by complex variables .![]()
![]()
[ Convergence of power series in the complex plane ] If the power series
![]()
Converging absolutely inside the circle and divergent outside the circle, then the converging circle called the series is the radius of convergence, and![]()
![]()
![]()
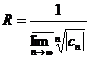
or
![]()
[ Abel's theorem ] For every power series
![]()
There exists a radius of convergence ( ) with the following properties:![]()
![]()
1 oFor every point inside , the series converges absolutely . On every closed circle ( ), the series converges uniformly . ![]()
![]()
![]()
![]()
2o , the series diverges . ![]()
Including 3o , the sum of the series is an analytic function . ![]()
From the property 3 o and the Taylor series expansion theorem, it can be known that the complex variable function can be expanded to a power series analytically at a point and in the neighborhood of the point .![]()
![]()
[ Operation rules ] In the common convergence circle , there are the following operation rules:![]()
![]()
![]()
( )![]()
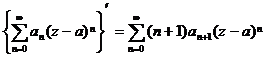
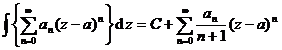
( is any plural)![]()
2. Laurent series expansion theorem
If the function is resolved in the annular region ( , ), then it can be expanded into a Laurent series in the annular region![]()
![]()
![]()
![]()
![]()
![]()
in the formula
![]() ,
, ![]()
![]() is any circle ( ), and the Laurent series of the function converges uniformly on any closed region in the annular region .
is any circle ( ), and the Laurent series of the function converges uniformly on any closed region in the annular region .![]()
![]()
![]()
The series is called the regular part of the Laurent expansion,![]()
The series is called the main part of the Laurent expansion .![]()
If the series converges in the annular region , then the sum of the series is analytic in this region, and this series is the Laurent series . Therefore, the Laurent expansion of the analytic function on the torus is unique .![]()
![]()
![]()
![]()
3. Local properties of analytic functions
[ The zero point of the analytic function ] is set in the analytic, and is called the zero point of . If it is , then it is called the order zero point of![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The zeros of analytic functions are isolated, that is, if they are zeros, and they are not , then there must be a positive number such that there are no other zeros except inside the circle .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Uniqueness theorem of analytic functions ] Let the function sum be analytic in the region , the interior point list ( ) of a limit point belongs to , if![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
then in the area![]()
![]()
This property indicates that the analytic function in the region is completely determined by the value on the point sequence of any interior point that converges to .![]()
![]()
![]()
[ Isolated singularity (removable singularity, pole, intrinsic singularity) ] If the function is analyzed except in a neighborhood of , it is called an isolated singularity of the function . The isolated singularity is divided into three categories:![]()
![]()
![]()
![]()
![]()
![]()
1 o When ( is a finite number), it is called a de-removable singularity . The necessary and sufficient conditions for a de-singularity of yes are: the Laurent series of * in the neighborhood of Domains are bounded .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2 o is called the pole of . The sufficient and necessary condition of the pole of y is: the main part of the Laurent series in the neighborhood of , contains only finite polynomials, namely
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If the principal part has the highest negative power , then it is called the order pole of .![]()
![]()
![]()
![]()
![]()
3 o When it does not exist, it is called the intrinsic singularity of . The necessary and sufficient condition for the intrinsic singularity of the function is that the main part of the Laurent series in the neighborhood of y has infinite polynomials .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If it is the inherent singularity of the function f ( z ) , then for any complex number A , there exists a sequence , , such that![]()
![]()
![]()
![]()
![]()
[ Taylor's theorem ] If the function is resolved in the region , then for the inner point , we have![]()
![]()
![]()
![]()
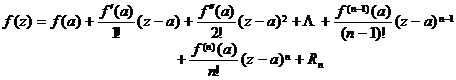
where the remainder is of the form
![]()
C is the circumference ( within the interior ) of the center of the circle .![]()
![]()
![]()
Taylor's theorem is about finite expansions of analytic functions, and Taylor's series expansion theorems (§ 4 , 1, 1 ) are in infinite series form . For studying the local properties of analytic functions, the finite expansions here are useful .
[ Properties of Analytical Functions at Infinity ]
1 o The neighborhood of an infinity point is centered on the origin and all points outside a circle of radius are a neighborhood of the infinity point . ![]()
2 o The infinity point is an isolated singularity set . If it can go to a singularity, then it is called a reversible singularity; if it is a first-order pole, it is called a first-order pole; if it is an inherent singularity, then called the singularity of nature . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3 The Laurent series in the neighborhood where the Laurent series of the o function is set at infinity is ![]()
![]()
![]()
![]()
Let , get the Laurent series in the neighborhood of![]()
![]()
![]()
![]() , )
, ) ![]()
![]()
Therefore, when yes , the Laurent series does not contain positive powers when it can go to the singularity; when yes , there are only positive powers of finite terms in the Laurent series , and ( ) is The last coefficient not equal to zero; when is an intrinsic singularity of , there are infinitely many positive powers in the Laurent series of .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4 The property of the o function is an isolated singularity at the infinite point. When it is a singular point, the modulus of the function is bounded in a certain neighborhood of the infinite point; when it is a pole of order, the modulus of the function is infinity. is unbounded in any neighborhood of the far point; when it is an inherently singular point, for any complex number , there exists a point sequence , , such that . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5 o The point at infinity is the zero point of the positive power not contained in the Laurent series, and . If , and ( ), then the point at infinity is said to be the zero point of order . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Classification of single-valued analytic functions
A function that has no singularities in the whole plane (excluding ) is called an integral function (holomorphic function) .![]()
A function that has no other singularities in the full plane (excluding the poles) is called a fractional function (semi-pure function or meromorphic function)![]()
5. Partial Fractional Expressions of Semipure Functions
![]()
![]()
![]()
![]()
![]()
![]()
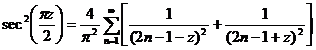
![]()
Second,
the residue theorem and its applications
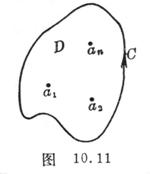
[ Definition of Residue ] Suppose a point is an isolated singularity of a function, a circle , called an integral![]()
![]()
![]()
![]()
![]()
The value of is the residue (residual) of the function at the isolated singularity , denoted as , here is a suitably small positive number (so that there are no other singularities in the circle), and the residue value has nothing to do with the value of .![]()
![]()
![]()
![]()
![]()
![]()
The residue of the function at an isolated singularity is equal to the coefficient of the negative first power in the Laurent expansion in the neighborhood of the point , i.e.![]()
![]()
![]()
![]()
![]()
[ Residue calculation rule for isolated singularities ]
1 The residue of the o function at the de-singularity is zero .
2 o Let be the first-order pole, then ![]()
![]()
![]()
3 o Let be the order pole point, then ![]()
![]()
![]()
![]()
4 o Let the fractional function , and analytically at point , be the first-order zero point, and then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ( for the derivative of in)
( for the derivative of in)![]()
![]()
![]()
5. Let o be an isolated singularity, which represents a circle with a sufficiently large radius (so that there are no other singularities outside the circle ), and the integral is called ![]()
![]()
![]()
![]()
![]()
![]()
The value of is the residual (which is taken clockwise), denoted as , so![]()
![]()
![]()
![]()
![]()
[ Residue Theorem ] If the function is analytic except for a finite number of singularities in the interior of a simple closed curve , and is continuous except on the above , then![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Argument principle ] If the function is analyzed in the interior of a simple closed curve except for a finite number of poles of order, it is continuous except for points on the upper, and there are no zeros and poles on the upper, and there are zeros of order in the inner , then![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Among them, it represents the change of the argument after the point moves one circle along the curve . If it is the image of the curve under the mapping, it is called the number of revolutions of the curve .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Rucher's Theorem ] If the function sum is analytic inside a simple closed curve sum, and![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
Then inside, and have the same number of zeros, that is![]()
![]()
![]()
![]()
[ Using Residue Theorem to Calculate Definite Integral ]
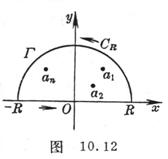
1 o Calculate points ![]()
if it is analytic everywhere on the upper half-plane including the real axis, except for a finite number of isolated singularities above the real axis, while assuming yes to zeros of at least second order, or![]()
![]()
![]()
![]()
![]() ( , is a constant)
( , is a constant)![]()
![]()
The integral can then be calculated as follows (Figure 10.12 ):![]()
(1)
As an auxiliary function , on the real axis![]()
![]()
(2)
Make an additional integral route so that the sum becomes a closed curve containing all singularities , then![]()
![]()
![]()
![]()
![]()
![]()
(3)
Find the sum of the residues of each singularity in the upper half-plane, and apply the residue theorem, we have![]()
![]()
(4)
Let , according to the assumption, , then![]()
![]()
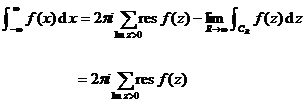
Example 1
calculation ![]()
untie
![]()
(1) As an auxiliary function .![]()
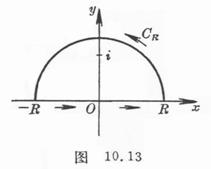
(2) Make an additional integral line : take the origin as the center and the upper half of the circle with a sufficiently large radius (Figure 10.13 ) .![]()
![]()
|
|
(3) There is only one pole in the upper half plane , and the residue is![]()
![]()
![]()
( 4 )
![]()
so
![]()
2 o Calculate the integral ( )
![]()
![]()
Let be a rational function with the degree of the denominator and the degree of the numerator ( ) .![]()
![]()
![]()
![]()
The basic steps of the calculation are the same as above, and its auxiliary function is that the additional integral route and integral closed curve are divided into the following two cases:![]()
![]()
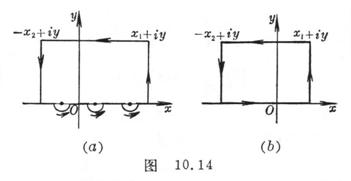
(a) If there are a finite number of first-order poles on the real axis, the integral closed curve (at the poles, with each pole as the center and radius as a semicircle on the lower half plane, is positive) is shown in Figure 10.14 ( a ) * , then![]()
![]()
![]()
|
|
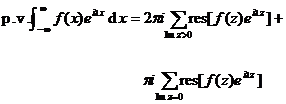
The generalized integral here is the Cauchy principal value, which is defined in Chapter VI § 1 , 5 .
(b) If there are no odds on the real axis![]()
point, the integral closed curve is shown in Figure 10.14 ( b ) .
![]()
Example 2 Calculate the integral ( )![]()
![]()
The solution is an auxiliary function , which has only two singularities on the real axis , , so by ( a )
![]()
![]()
![]()
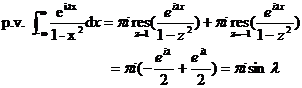
Example 3 Calculate the integral![]()
Solution ( 1 ) is used as an auxiliary function .![]()
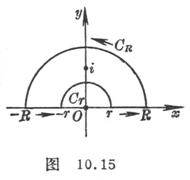
( 2 ) Do the sum and sum of the additional integral lines , and together they become a closed curve containing singular points (Fig. 10.15 ), then![]()
![]()
![]()
![]()
![]()
![]()
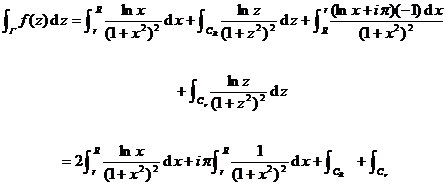
|
|
( 3 ) There is only one second-order pole in the function in the curve . According to the residual calculation rule 3o of the isolated singular point, the residual at the obtained place is then![]()
![]()
![]()
![]()
![]()
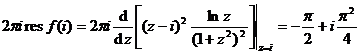
( 4 ) It can be proved that when , when, integral , , then we get![]()
![]()
![]()
![]()
![]()
The real parts of both sides of the above equation are equal, so
![]()