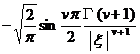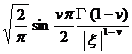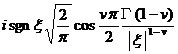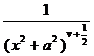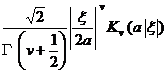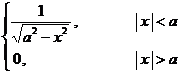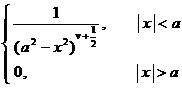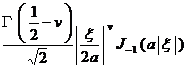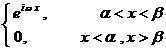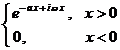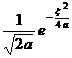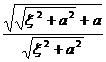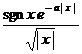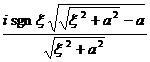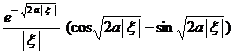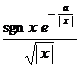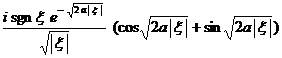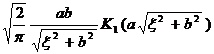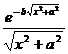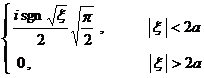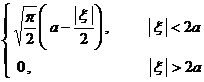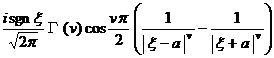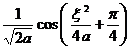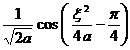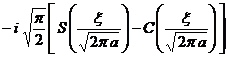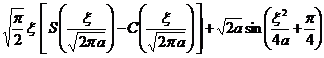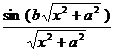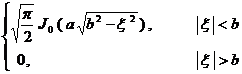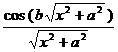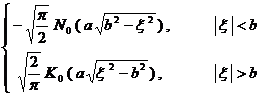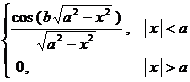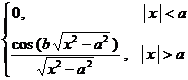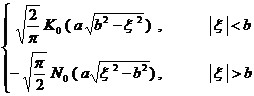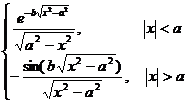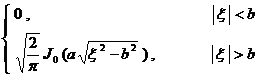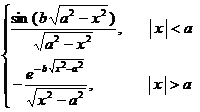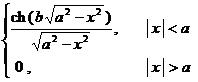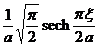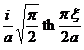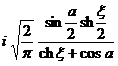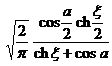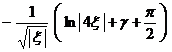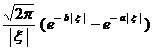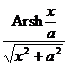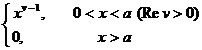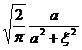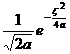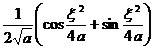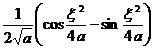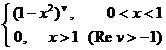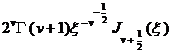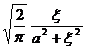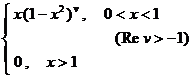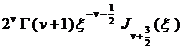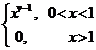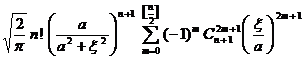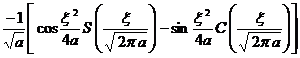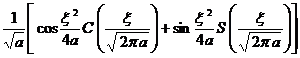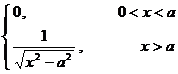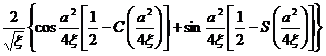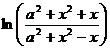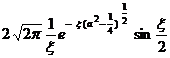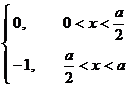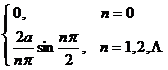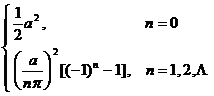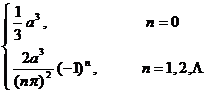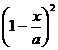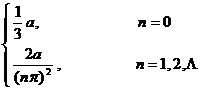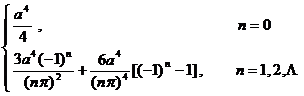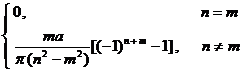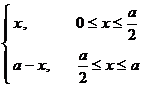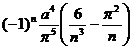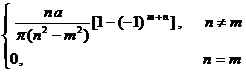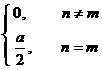§4   Fourier Transform

 

1. Fourier integral 

 

    [ Fourier integral ]   A function that is absolutely integrable over any finite interval [- l , l ] , its Fourier series can be found ( §1 , 2 of this chapter )

                                       (1)

    Assuming that the function is absolutely integrable over the infinite interval (- ) , in equation (1) , let l , obtain the Fourier integral of f ( x )

    [ Several forms of Fourier integral ]

    Let the Fourier integral satisfy the convergence condition, then

    1 ^o = 

    2 ^o = (     outer integral is understood as integral in the sense of principal value )

    3 ^o  is an even function:

=

    4 ^o  is an odd function:

=

    [ Convergence discriminant method of Fourier integral ] Assuming that the   function is absolutely integrable, the imaginary value of the integral (1) is S ₀ . Suppose that the point x ₀ is continuous, or x ₀ is its first-type discontinuous point, and the continuous point is At point x ₀ S ₀ = , while at the first type of discontinuity point x ₀ ,

S ₀ =

    1 ^o  Dini discriminant decree , if for a , the integral

converges, then the Fourier integral converges at the point x ₀ and is equal to S ₀ .

    2 ^o  Dirichlet - Rawdang discriminant If there is a bounded variation on an interval [ x ₀ - h , x ₀ + h ] with x ₀ as the midpoint, then its Fourier integral is at the point x ₀ converges and is equal to S ₀ . 

    3 ^o  If the function has bounded variation on, while

Then the Fourier integral converges at any point x _{0 and is equal to} S ₀ .

 

2. Fourier transform

 

    The Fourier transform of [ Fourier transform and its inversion formula ]   is

    The inversion formula of the Fourier transform is

    The Fourier transform and inversion formula of [ Conditions for the existence of Fourier transform ] are meaningful   ( only at the discontinuity point x ₀ of ) under the following two conditions, and the left end of the inversion formula should be equal to ):

    1 ^o  exists;

    2 ^o  satisfies the Dirichlet condition: there are only a finite number of extreme points and only a finite number of discontinuities of the first kind .

    [ Properties of Fourier Transform ]   Let the Fourier transform of g ( x ) be F ( ) and G ( ) respectively, then

    1 ^o  The Fourier transform of a linear a + b g ( x ) is a F ( ) + b G ( ) ( a , b are constants )            

    2 ^o  The Fourier transform of convolution ( or convolution ) f ( x )*g( x )=     is

F ( ) G ( )

    3 ^o  Parsepha equation  

    4 ^o  The Fourier transform of the flip f ( -x ) is F (- ).          

    The   Fourier transform of the 5o ^conjugate is .            

      The Fourier transform of ^6o time - shift ( delay )    f ( x - x ₀ ) is .   

7o ^frequency  shift ( frequency modulation )    is the Fourier transform of ( is a constant ).   

 

    [ Fourier transform table ]

         , 

	( g is Euler's constant )

 

3. Fourier cosine transform

 

    [ Fourier cosine transform and its inversion formula ]   The Fourier cosine transform of f ( x ) is

    The inversion formula of the Fourier cosine transform is:

    [ Existence condition of Fourier cosine transform ]   is the same as the Fourier integral convergence condition .

    [ Properties of Fourier Cosine Transform ]

    1 ^o  If it is the Fourier cosine transform of f ( x ) , then it is the Fourier cosine transform of .

    2 ^o  If f ( x ) is an even function, then .

       The Fourier cosine transform of 3 ^o ( a > 0) is .

    [ Fourier cosine transform table ]

, 

 

Four, Fourier sine transform

 

    [ Fourier sine transform and its inversion formula ]   The Fourier sine transform of f ( x ) is

    The inversion formula of the Fourier sine transform is

    [ Existence condition of Fourier sine transform ]   is the same as the Fourier integral convergence condition .

    [ Properties of Fourier Sine Transform ]

    1 ^o  If it is the Fourier sine transform of f ( x ) , then it is the Fourier sine transform of .

    2 ^o  If f ( x ) is an odd function, then .

       The Fourier sine transform of 3 ^o ( a > 0) is .

    [ Fourier sine transformation table ]

,  

	( for Euler's constant )

 

5. Finite Fourier Cosine Transform

 

    [ Finite Fourier cosine transform and its inversion formula ]   Let f ( x ) satisfy the Dirichlet condition in the interval ( see this section, two ) , then the finite Fourier cosine transform of f ( x ) is

    The inversion formula of the finite Fourier cosine transform is:

    at each successive point of f ( x ) in the interval

At the discontinuity, the left-hand side of the equation is changed to .

    [ Finite Fourier Cosine Transform Table ]

,  

1
	,
( m is an integer )

 

6. Finite Fourier Sine Transform

 

    [ Finite Fourier sine transform and its inversion formula ]   Let f ( x ) satisfy the Dirichlet condition in the interval ( see this section, 2 ) , then the finite Fourier sine transform of f ( x ) is

    The inversion formula of the finite Fourier sine transform is:

    at each successive point of f ( x ) on the interval

At the discontinuity, the left-hand side of the equation is changed to .

    [ Finite Fourier Sine Transform Table ]

,  

1
	,
( m is an integer )
( m is an integer )

 

Seven, double Fourier transform and its inversion formula

 

    The double Fourier transform of f ( x , y ) is

    The inversion formula of the double Fourier transform is: