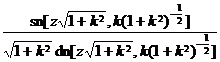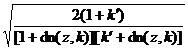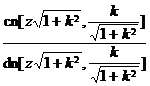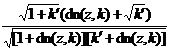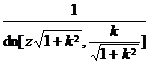§ 6
Elliptic functions
First,
the definition and properties of elliptic functions
Semi-pure functions with two periods are called elliptic functions .
|
|
If and are the two fundamental periods (also called primitive periods) of the elliptic function , for any integer we have![]()
![]()
![]()
![]()
![]()
![]()
by
![]()
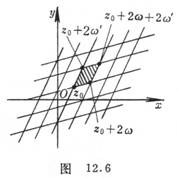
A parallelogram whose vertices are any complex number is called![]()
Periodic parallelogram . The entire plane can form such a circle![]()
period parallelogram net (Figure 12.6 ) .
![]() within a periodic parallelogram (including two
within a periodic parallelogram (including two
Adjacent edges and their intersections) the number of poles (the number of poles and the number of zeros)
The numbers are equal, and the order poles are counted as a) is called the order of an elliptic function. An elliptic function of order is called an order elliptic function .![]()
![]()
![]()
![]()
Elliptic functions have the following properties:
![]() The sum, difference, product, quotient and derivative of elliptic functions with the same period are elliptic functions with the same period .
The sum, difference, product, quotient and derivative of elliptic functions with the same period are elliptic functions with the same period .
![]() Elliptic functions that are not constants must have poles .
Elliptic functions that are not constants must have poles .
The quotient of an elliptic function with the same period, zeros, and poles (zeros and poles are also of the same order) is a constant .
Elliptic functions with the same period, the same poles, and the same major part at each pole differ by a constant .
![]() The sum of the residues of an elliptic function at all poles in its periodic parallelogram is zero .
The sum of the residues of an elliptic function at all poles in its periodic parallelogram is zero .
![]() The order of the elliptic function is at least equal to 2.
The order of the elliptic function is at least equal to 2.
![]() Within a periodic parallelogram, the elliptic function takes each (finite or infinite) value the same degree and equal to the order of the elliptic function .
Within a periodic parallelogram, the elliptic function takes each (finite or infinite) value the same degree and equal to the order of the elliptic function .
![]() The difference between the sum of all zeros and the sum of all poles of an elliptic function in a periodic parallelogram is equal to a certain period of it, namely
The difference between the sum of all zeros and the sum of all poles of an elliptic function in a periodic parallelogram is equal to a certain period of it, namely
![]()
In the formula, the zero point is the pole point, and it is a certain integer .![]()
![]()
![]()
Second,
the Jacobi elliptic function
[ Definition and series expression of Jacobi elliptic function ]
Elliptic integrals of the first kind
![]()
The inverse function of is a two-period meromorphic function, denoted by
![]()
It has basic cycles:
![]()
![]()
![]()
![]() is called the elliptic sine, and it is called the modulus in the formula, and it is called the complementary modulus . If
is called the elliptic sine, and it is called the modulus in the formula, and it is called the complementary modulus . If![]()
![]()
![]()
is called the amplitude function, denoted as . Also defined![]()
![]()
![]()
![]() (called elliptic cosine)
(called elliptic cosine)
![]() (called elliptic tangent)
(called elliptic tangent)
![]()
![]() They are collectively referred to as Jacobi elliptic functions . They are all second-order elliptic functions .
They are collectively referred to as Jacobi elliptic functions . They are all second-order elliptic functions .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ special point value ]
|
|
|
|
|
|
|
|
|
|
|
0 1 1 |
|
1 0
|
|
|
|
0 |
[ Period , Zero , Pole , Residue ]
|
|
basic cycle |
zero |
pole |
residue _ |
|
|
|
|
|
|
[ induction formula table ]
![]()
|
n m |
-1 |
0 |
1 |
2 |
2p _ |
|
-1 0 |
|
|
|
|
|
|
n m |
-1 |
0 |
1 |
2 |
2p _ |
|
1 2 |
|
|
|
|
|
|
2q _ |
|
|
|
|
|
![]()
|
n m |
-1 |
0 |
1 |
2 |
2p _ |
|
-1 0 1 2 |
|
|
|
|
|
|
2q _ |
|
|
|
|
|
![]()
|
n m |
-1 |
0 |
1 |
2 |
p |
|
-1 0 1 2 |
|
|
|
|
|
|
q |
|
|
|
|
|
[ Conversion formula ]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ Basic relationship ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Addition formula ]
![]()
![]()
![]()
[ Multiple formula ]
![]()
![]()
![]()
![]()
![]()
[ Half formula ]
![]()
![]()
![]()
[ Multiplication formula ]
![]()
![]()
![]()
![]()
[ Derivative and integral formulas ]
![]() , ,
, , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.
Weylstras elliptic function
Elliptic integrals of the first kind by Weylstras
![]()
The inverse function of is called the Weylstras elliptic function,![]()
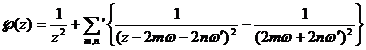
In the formula, it means to sum up all integers except), in the neighborhood of , there are![]()
![]()
![]()
![]()
The Weylstras elliptic function has the following properties:
![]()
![]() is a second-order elliptic function with a second-order pole in a periodic parallelogram:
is a second-order elliptic function with a second-order pole in a periodic parallelogram:![]()
![]() .
.
![]()
![]() The period is and is any integer) .
The period is and is any integer) .![]()
![]()
![]()
![]()