§4 偏微分方程的数值解法
一、 差分法
差分法是常用的一种数值解法.它是在微分方程中用差商代替偏导数,得到相应的差分方程,通过解差分方程得到微分方程解的近似值.
1. 网格与差商
|
图14.7 |
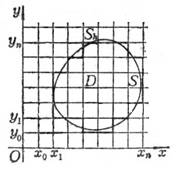
在平面 (x,y)上的一以S为边界的有界区域D上考虑定解问题.为了用差分法求解,分别作平行于x轴和y轴的直线族.
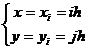 (i,j=0,1,2,…,n)
(i,j=0,1,2,…,n)
作成一个正方形网格,这里h为事先指定的正数,称为步长;网格的交点称为节点,简记为(i,j).取一些与边界S接近的网格节点,用它们连成折线Sh,Sh所围成的区域记作Dh.称Dh内的节点为内节点,位于Sh上的节点称为边界节点(图14.7).下面都在网格Dh + Sh上考虑问题:寻求各个节点上解的近似值.在边界节点上取与它最接近的边界点上的边值作为解的近似值,而在内节点上,用以下的差商代替偏导数:
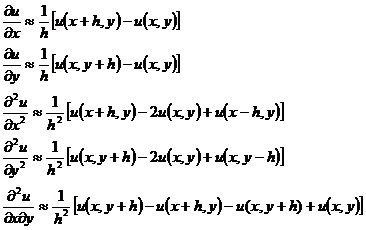
注意, 1° 式中的差商![]() 称为向后差商,而
称为向后差商,而![]() 称为向前差商,
称为向前差商,![]() 称为中心差商.也可用向前差商或中心差商代替一阶偏导数.
称为中心差商.也可用向前差商或中心差商代替一阶偏导数.
2° x轴与y轴也可分别采用不同的步长h,l,即用直线族
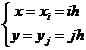 (i,j=0, ±1, ±2
(i,j=0, ±1, ±2![]() )
)
作一个矩形网格.
2. 椭圆型方程的差分方法
[五点格式] 考虑拉普拉斯方程的第一边值问题
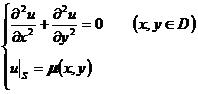
式中(x,y)为定义在D的边界S上的已知函数.
采用正方形网格,记u(xi,yj)=uij ,在节点(i,j)上分别用差商
![]()
代替![]() ,对应的差分方程为
,对应的差分方程为
![]() (1)
(1)
或
![]()
即任一节点(i,j)上uij的值等于周围相邻节点上解的值的算术平均,这种形式的差分方程称为五点格式,在边界节点上取
![]() (2)
(2)
式中(xi*,yj*)是与节点(i,j)最接近的S上的点.于是得到了以所有内节点上的uij值为未知量的若干个线性代数方程,由于每一个节点都可列出一个方程,所以未知量的个数与方程的个数都等于节点的总数,于是,可用通常的方法(如高斯消去法)解此线性代数方程组,但当步长不很大时,用高斯消去法将会遇到很大困难,可用下面介绍的其他方法求解.
若h0时,差分方程的解收敛于微分方程的解,则称差分方程为收敛的.
在计算过程中,由于进行四则运算引起舍入误差,每一步计算的舍入误差都会影响以后的计算结果,如果这种影响所产生的计算偏差可以控制,而不至于随着计算次数的增加而无限增大,则称差分方程是稳定的.
[迭代法解差分方程] 在五点格式的差分方程中,任意取一组初值{uij},只要求它们在边界节点(i,j)上取以已知值(xi*,yj*),然后用逐次逼近法(也称迭代法)解五点格式:
![]()
逐次求出{uij(n)}.当(i+1,j),(i-1,j),(i,j-1),(i,j+1)中有一点是边界节点时,每次迭代时,都要在这一点上取最接近的边界点的值.当n∞时,uij(n)收敛于差分方程的解,因此n充分大时,{uij(n)}可作差分方程的近似解,迭代次数越多,近似解越接近差分方程的解.
[用调节余数法求节点上解的近似值] 以差商代替Δu时,用节点(i+1,j),(i-1,j),(i,j+1),(i,j-1)上u的近似值来表示u在节点(i,j)的值将产生的误差,称此误差为余数Rij,即
![]()
|
图14.8 |
设在(i,j)上给uij以改变量uij,从上式可见Rij将减少4uij,而其余含有u(xi,yj)的差分方程中的余数将增加uij,多次调整uij的值就可将余数调整到许可的有效数字的范围内,这样可获得各节点上u(x,y)的近似值.这种方法比较简单,特别在对称区域中计算更简捷.
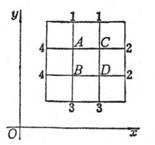
例
求Δu=0在内节点A,B,C,D上解的近似值.设在边界节点1,2,3,4上分别取值为1,2,3,4(图14.8)
解
记u(A)=uA,点A,B,C,D的余数分别为
-4uA+
uB+ uc +5=RA
uA-4 uB
+ uD+7=RB
uA
-4 uc+ uD+3=RC
uB+ uc-4uD+5=RD
以边界节点的边值的算术平均值作为初次近似值,即
uA(0)=uB(0)=uC(0)=uD(0)=2.5
则相应的余数为:
RA=0, RB=2, RC= -2,
RD=0
最大余数为±2.先用δuC=-0.5把RC缩减为零,uC相应地变为2,这时RA, RD也同时缩减(-0.5),新余数是RA=-0.5,RB=2,![]() , RD=-0.5.类似地再变更δuB=0.5,从而 uB变为3,则得新余数为
, RD=-0.5.类似地再变更δuB=0.5,从而 uB变为3,则得新余数为![]() .这样便可消去各节点的余数,于是u在各节点的近似值为:
.这样便可消去各节点的余数,于是u在各节点的近似值为:
uA=2.5, uB=3, uC=2, uD=2.5
现将各次近似值及余数列表如下:
|
次数 |
调 整 值 |
第n次近似值及余数 |
|||||||
|
uA |
RA |
uB |
RB |
uC |
RC |
uD |
RD |
||
|
0 1 2 |
δuC = -0.5 δuB = 0.5 |
2.5 2.5 2.5 |
0 -0.5 0 |
2.5 2.5 3 |
2
2 0 |
2.5 2 2 |
-2 0 0 |
2.5 2.5 2.5 |
0 -0.5 0 |
|
结果近似值 |
2.5 |
|
3 |
|
2 |
|
2.5 |
|
|
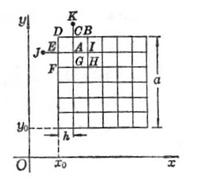
[解重调和方程的差分方法] 在矩形D(x0≤x≤x0+a,y0≤y≤y0+a)中考虑重调和方程
![]()
取步长![]() ,引直线族
,引直线族
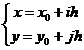 (i, j = 0, 1, 2
(i, j = 0, 1, 2![]() n)
n)
作成一个正方形网格.用差商代替偏导数
|
图14.9 |

上式表明了以(x,y)为中心时,u(x,y)的函数值与周围各点函数值的关系,但对于邻近边界节点的点(x,y),如图14.9中的A,就不能直接使用上式,此时将划分网格的直线族延伸,在延伸线上定出与边界距离为h的点,称这些点为外邻边界节点,如图14.9以A为中心时,点E,C为边界节点,点J,K为E,C的外邻边界节点,用下法补充定义外邻边界节点J处函数的近似值uJ,便可应用上面的公式.
1° 边界条件为
![]()
时,定义uJ=uA-22(E)h.
2° 边界条件为
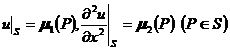
时,定义uJ=21(E)-uA-h22(E).
[其他与Δu有关的网格]
1° 三角网格(图14.10(a))
取P0(x,y)为中心,它的周围6个邻近节点分别为:
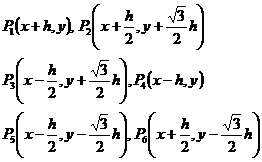
则 ![]()
式中ui=u(Pi),
u0=u(P0),R表示余项.
2° 六角网格(图14.10(b))
取P0(x,y)为中心,它的三个邻近节点分别为
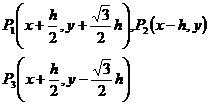
则
![]() .
.
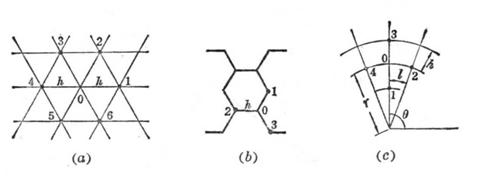
图14.10
3° 极坐标系中的网格(图14.10(c))
取P0(r,![]() )为中心,它的四个邻近节点分别为
)为中心,它的四个邻近节点分别为
![]()
而拉普拉斯方程
![]()
的相应的差分方程为
![]()
3. 抛物型方程的差分方法
考虑热传导方程的边值问题
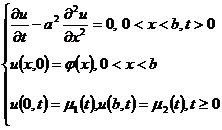
将[0,b]分为n等份,每段长为![]() .引两族平行线(图14.11)
.引两族平行线(图14.11)
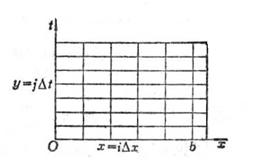
图14.11
x=xi=ix (i=0,1,2![]() n)
n)
y=yj=jt (j=0,1,2![]() t 取值见后)
t 取值见后)
作成一个长方形的网格,记u(xi,tj)为uij,节点(xi,tj)为(i,j),在节点(i,j)上分别用
![]()
代替![]() ,于是边值问题化为差分方程
,于是边值问题化为差分方程
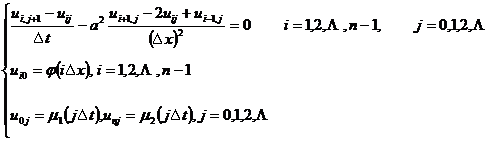
记![]() ,差分方程可写成
,差分方程可写成
![]() (1)
(1)
由此可按t增加的方向逐排求解.在第0排上ui0的值由初值(ix)确定,j+1排ui,j+1的值可由第j排的三点(i+1,j),(i,j),(i-1,j)上的值ui+1,j, uij,ui-1,j确定,而u0,j+1,un,j+1已由边界条件1((j+1)t)及2((j+1)t)给定,于是可逐排计算一切节点上的uij值.当(x), 1(x)和2(x)充分光滑,且![]() 时,差分方程收敛而且稳定.所以利用差分方程(1)计算时,必须使
时,差分方程收敛而且稳定.所以利用差分方程(1)计算时,必须使![]() ,即
,即![]() .
.
热传导方程还可用差分方程
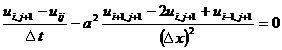
代替,此时如已知前j排uij的值,为求第j+1排的ui,j+1
必须解包含n-1个未知量![]() 的线性代数方程组,这种差分方程称为隐式格式的差分方程,前面所提的差分方程称为显式格式差分方程.
的线性代数方程组,这种差分方程称为隐式格式的差分方程,前面所提的差分方程称为显式格式差分方程.
隐式格式差分方程对任意的λ都是稳定的.
4. 双曲型方程的差分方法
考虑弦振动方程的第一边值问题
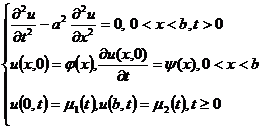
用矩形网格,列出对应的差分方程:
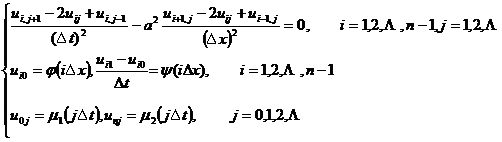
记![]() 与上段一样,利用
与上段一样,利用![]() 和在第0排及第1排的已知数值(初始条件)ui0 ,
ui1可计算ui2,然后用已知的ui1 ,
ui2及
和在第0排及第1排的已知数值(初始条件)ui0 ,
ui1可计算ui2,然后用已知的ui1 ,
ui2及![]() 可计算ui3,类似地可确定一切节点上的uij值.
可计算ui3,类似地可确定一切节点上的uij值.
当(x),(x),1(x)和2(x)充分光滑,且ω≤1时,差分方程收敛且稳定,所以要取![]() .
.
二、 变分方法
1. 自共轭边值问题
将§3定义的共轭微分算子的概念推广到一般方程.
设D是![]() 中的有界区域,S为其边界,在
中的有界区域,S为其边界,在![]() 上考虑2k阶线性微分方程
上考虑2k阶线性微分方程
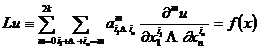
的齐次边值问题
![]()
式中f(x)是D内的已知函数,lju是线性微分算子.
将 ![]() 分部积分k次得
分部积分k次得
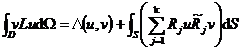
式中(u,v)是一个D上的积分,其被积函数包含u,v的k阶导数;Rj和![]() 是定义在边界S上的两个线性微分算子.再将(u,v)分部积分k次得
是定义在边界S上的两个线性微分算子.再将(u,v)分部积分k次得
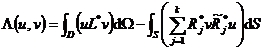
式中L*是一个2k阶的微分算子,称为L的共轭微分算子.若L=L*,则称L为自共轭微分算子.从上面可推出格林公式
![]()
如从lju|S=ljv|S=0可推出在边界S上
![]()
则称lju|S=0为自共轭边界条件.如果微分算子及边界条件都是自共轭的,则称相应的边值问题为自共轭边值问题,此时有
![]()
每个边值问题对应于某希尔伯特空间H(例如L2(D),见第九章§7)中的一个算子A,其定义域MA 是H中一线性稠密集合,它由足够次连续可微且满足边界条件的函数组成,在MA上,Au的数值与Lu的数值相同,从而求解边值问题化为解算子方程
![]()
的问题.
设A为定义在实的希尔伯特空间H中的某线性稠密集合MA上的线性算子.若对于MA的任意非零元素![]() 成立
成立
(Au,v)=(u,Av)
则称A为对称算子.若对任意非零元素u成立
![]()
则称A为正算子.如成立更强的不等式
(Au,u)≥r||u||2 (r>0)
则称A为正定算子.此处(u,v)表示希尔伯特空间的内积,||u||2=(u,u).
2. 变分原理与广义解
定理
设A是正定算子,u是方程Au=f在MA上的解的充分必要条件是: u使泛函
F(u)=(Au,u)-2(f,u)
取极小值.
上述将边值问题化为等价的求泛函极值问题的方法称为能量法.在算子的定义域不够大时,泛函F(u)的极值问题可能无解.不过对于正定算子,可以开拓集合MA,使在开拓了的集合上,泛函的极值问题有解.为开拓MA,在MA上引进新的内积[u,v]=(Au,v),定义模||u||2=[u,u]=(Au,u),在模||u||的意义下,补充极限元素,得到一个新的完备希尔伯特空间H0,在H0上,泛函F(u)仍然有意义,而泛函的极值问题有解.但必须注意,此时使泛函F(u)取极小的元素u0不一定属于MA,因此它不一定在原来的意义下满足方程Au=f及边界条件.称u0为广义解.
3. 极小化序列与里兹方法
在处理变分问题中,极小化序列起着重要的作用.考虑泛函
F(u)=(Au,u)-2(f,u)
以d表示泛函的极小值.设在希尔伯特空间中存在一列元素{un}
(n=1,2![]() ),使
),使
![]()
则称{un}为极小化序列.
定理
若算子A是正定的,则F(u)的每一个极小化序列既按H空间的模也按H0的模收敛于使泛函F(u)取极小的元素.
这个定理不但指出利用极小化序列可求问题的解,而且提供一种近似解的求法,即把极小化序列中的每一个元素当作问题的近似解.
设算子A是正定的,构造极小化序列的里兹方法的主要步骤是:
(1) 在线性集合MA中选取H0中完备的元素序列{i} ,
(i=1,2![]() ) 并要求对任意的n,1,2,…,n线性无关.称这样的元素为坐标元素.
) 并要求对任意的n,1,2,…,n线性无关.称这样的元素为坐标元素.
(2) 令![]() ,其中ak为待定系数.代入泛函F(u),得自变量a1,a2,…,an的函数
,其中ak为待定系数.代入泛函F(u),得自变量a1,a2,…,an的函数
![]()
(3) 为使函数F(un)取极小,必须![]() ,从而求出ak (k=1,2,…,n).序列{un}即为极小化序列,un可作为问题的近似解.
,从而求出ak (k=1,2,…,n).序列{un}即为极小化序列,un可作为问题的近似解.
4. 里兹方法在特征值问题上的应用
算子方程
Au-u=0
的非零解称为算子A的特征值,对应的非零解u称为所对应的特征函数.
对线性算子A,若存在常数K,使对任何MA的元素成立
(A,)≥K||||2
则称A为下有界算子,正定算子是下有界的(此时K=0).记(A,)/||||2的下确界为d.
定理1 设A为下有界对称算子,若存在不为零的元素0MA,使
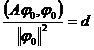
则d就是A的最小特征值,0为对应的特征函数.
于是求下有界对称算子的最小特征值问题化为变分问题,即在希尔伯特空间中求使泛函(A,)/||||2取极小的元素,或在||||=1的条件下求使泛函(A,)取极小的元素.
Theorem 2 Let A be a lower bounded symmetric operator, 1 ≤ 2 ≤…≤ n be its first n eigenvalues, 1 , 2 , … , n are the corresponding standard orthogonal eigenfunctions, if there is a non-zero element , with additional conditions ![]()
( , )=1, ( , 1 )=0, ( , 2 )=0, … , ( , n )=0
Let the functional ( A , ) be minimized , then n + 1 is the eigenfunction of operator A , and the corresponding eigenvalue
![]()
It is the smallest eigenvalue other than 1 and n .![]()
So finding the n +1th eigenvalue becomes a variational problem, that is, in the additional condition
( , )=1, ( , 1 )=0, ( , 2 )=0 , ( ![]() , n )=0
, n )=0
Find the following so that the functional ( A , ) takes minimal elements .
In order to use the Ritz method to find the eigenvalues, select a sequence of coordinate elements { i }, ( i =1,2 ) in H 0 in M A , let , determine a k , so that under the conditions ( u n , u When n )=1 , ( Au n , u n ) is minimized, and this problem is reduced to the function of finding n variables a 1 , a 2 , … , a n
![]()
![]()
![]()
in condition
![]()
The extreme value problem under _
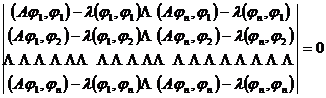
The smallest root of is the approximate value of the eigenvalue, if the roots of the above formula are arranged by size, the approximate value of the following eigenvalues can be obtained in turn, but the accuracy is poor .
For general operator equations
Au - Bu = 0
If A is a lower bounded symmetric operator and B is a positive definite operator, then
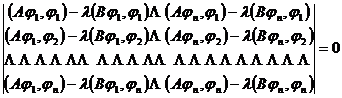
The root of is an approximation of the eigenvalue .
5. Kalyojin Method
There are many limitations in solving mathematical and physical problems with the Ritz method, the most important limitation is that the operator is required to be positive definite, but many problems do not necessarily meet this condition, and the Galerkin method makes up for this defect .
The main steps of the Kalyojin method are:
(1) Select a complete element sequence { i } ( i =1,2 ) in space H in M A , in which any n elements are linearly independent, and { i } ( i =1, 2, ... ) is called the coordinate sequence of elements . ![]()
(2) Express the approximate solution of the equation as
![]()
where a k is an undetermined constant, substitute u n into u in the equation Au=f , and take the inner product of both ends with j ( j =1,2, … , n ) to obtain n algebraic equations of a k
![]()
(3) Find a k , substitute back the expression of u n , then get the approximate solution of the equation u n .
In the self-conjugate boundary value problem, when the operator is positive, the system of algebraic equations for a k obtained by Galerkin's method and Ritz's method is the same .