§ 4 Approximate solution of integral equations
[ Approximation to the system of linear algebraic equations of the Fr equation ] Fr equation
![]() ( 1 )
( 1 )
available in form
![]()
![]() ( 2 )
( 2 )
to approximate, where x k ( k = 1,2, … , n ) are n appropriately selected quadrature nodes on the interval [ a , b ] and the constant ω k is the corresponding quadrature coefficient. If it is required that at each point x k ( k =1,2, … , n ) , both sides of equation ( 2 ) are equal, then about n unknown functions y ( x 1 ), y ( x 2 ), … y ( x n linear equations for n ) :
![]()
![]() ( 3 )
( 3 )
where y ( x i ) ( i =1,2, … n ) is the approximate value specified by the unknown function y ( x ) at n points x i ( i =1,2, … n ) respectively.
Ruo Ling
![]()
( 3 ) can be rewritten as
![]() ( i = 1, 2, … n )
( i = 1, 2, … n )
Written in matrix form as
y = F + λ KW y
or Ay = F ( 4 )
where A = I - λ KW , I is the n -order unit matrix, K = ( K ij ), W is the diagonal matrix
W = é w 1 , w 2 , L , w n û , y = ( y 1 , y 2 , L , yn ) t , F = ( F 1 , F 2 , L , F n ) t
Solve the Fr equation of the second kind by example
![]()
![]()
Solving for 1° In this special case, the integral equation can be reduced to a differential equation with endpoint conditions y (0)=0, y (1)=1
![]()
Its exact solution is
![]()
2° Use the approximation method to find an approximate solution. Take n = 5 equally spaced nodes:
![]()
The matrix K can be calculated as

If the trapezoidal method is used to obtain the product, then the diagonal matrix W of the product coefficients is
W = é û![]()
Since l = 1 , then
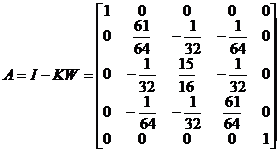
and ![]()
Solve a system of linear equations, and calculate to four decimal places to get
y 1 =0, y 2 = 0.2943, y 3 =0.5702, y 4 =0.8104, y 5 =1
with the exact solution y ( x ) at the point x = 0, and the value of 1![]()
y 1 =0, y 2 = 0.2940, y 3 =0.5697, y 4 =0.8100, y 5 =1
By comparing, you can see the degree of error.
The above method can obviously be used to find the approximate solution of the Fr equation of the first kind, and to deal with the problem of eigenvalues.
It should be noted that the above method is particularly useful when the kernel K ( x , x ) is not given in analytical expressions but determined from experimental data.
[ Undetermined coefficient approximation method ] In order to find the integral equation
![]() ( 1 )
( 1 )
The solution of , n functions can be selected appropriately , and their linear combination can be used to approximate![]()
![]()
where the n coefficients a k ( k = 1 , 2 , L n ) can be determined such that this linear combination satisfies ( 1 ) as approximately as possible, i.e.
![]() ( a ≤ x ≤ b )
( a ≤ x ≤ b )
make
![]()
The above formula becomes
![]() ( a ≤ x ≤ b ) ( 2 )
( a ≤ x ≤ b ) ( 2 )
Undetermined coefficients a 1 , a 2 , L , an n can be determined by n conditions, as follows:
1° Configuration Decree
![]()
![]() ( a ≤ x ≤ b ) ( 3 )
( a ≤ x ≤ b ) ( 3 )
In order to determine these n constants a 1 , a 2 , L , a n , appropriately choose a ≤ x 1 < x 2 < L < x n ≤ b on the interval [ a , b ] ( x i is called the configuration point ) , Make
![]() ( i =1,2, L n )
( i =1,2, L n )
Its matrix form is
y a = F (4)
where y =( ψ ij ) = ( ψ j ( x i )), F = ( F ( x 1 ), F ( x 2 ), L F ( x n )) τ is a known quantity,
a =( a 1, a 2,L, a n ) t
is an unknown quantity. Solving the system of linear equations ( 4 ) yields the required coefficients a 1 , a 2 , L , a n .
2° weight function method Let w 1 ( x ), w 2 ( x ), L , w n ( x ) be n linearly independent functions (called weight functions) on the interval [ a, b ] . In order to determine the coefficients a 1 , a 2 , L , an n , the difference between the two sides of equation ( 3 ) can be required
![]()
Orthogonal to these n weight functions, that is, we get
![]() ( i = 1, 2, … n )
( i = 1, 2, … n )
Its matrix form is
A a = b (5)
in the formula ![]()
![]()
![]()
is a known quantity,
a =( a 1, a 2,L, a n ) t
is an unknown quantity. Solving the system of linear equations ( 5 ) yields the required coefficients a 1 , a 2 , L , a n .
Usually, it is convenient to choose the identity of the weight function w i ( x ) and the approximate function ji ( x ) , which is generally taken as
1, x , x 2 , L , x n - 1
[ Approximation of Kernels ] § 1 states that the kernel of the Fr equation can be approximated by a polynomial of x and ξ or a separable kernel of a more general form, and the resulting approximate equations can be solved by methods there.
Example Integral Equation
![]() (1)
(1)
nucleus in
![]()
It can be approximated by the polynomial A 1 + A 2 x + A 3 x 2 or the more appropriate form x (1 - x )( B 1 + B 2 x + B 3 x 2 ) , where A , B are parameters including ξ , A and B can be determined using a weight function or configuration point .
First take a rough approximation
![]()
It is exact at the endpoints x = 0 and x = 1 , and to determine the coefficient B , it can be required that the integral of the kernel over [0,1] is equal to the integral of its approximate expression, i.e.
![]()
directly calculated
B = 3 ξ ( 1 - ξ )
And substitute the corresponding approximate kernel into (1) to derive the approximate integral equation
![]() (2)
(2)
make
![]()
(2) is transformed into
y ( x )= x +3 cx (1 - x ) (3)
To determine c , multiply both sides of the equation by x (1 - x ) and integrate over [0,1] to get
![]()
From this calculation , substitute into (3) to obtain the approximate solution of equation (1)![]()
![]()
More generally, if the approximate kernel is taken as
![]()
Then the approximate solution of equation (1) can be obtained similarly
![]() )
)