§ 5 Variation
1. Variation of functional and extremum of functional
[ Class function and 
neighborhood of curve ] A function with continuous derivatives is called a class function, and a function with an order continuous derivative is called a class function .
The neighborhood of a curve means that the inequality is satisfied in the whole interval
All possible curves of , then the curve is said to have zero-order proximity to the curve . If it also satisfies the inequality: , then the curve is said to have a first-order proximity to the curve, where .
[ Functional ] If for each function of a certain class of functions , there is a value corresponding to it, then the variable is called a function-dependent functional, denoted as .
[ Variation of a function] The variation of a variable of a functional refers to the difference between two functions: , where is a function belonging to the same function class .
[ Variation of the functional ] If the amount of change in the functional
can be expressed in the following form
where is linear for , and when , , then called the variation of the functional, denoted as . and have
[ Extreme value of functional ] If the value of the functional on any curve close to it is not less than , immediately , the functional reaches a minimum value on the curve . Similarly, the maximum value can be defined .
If the functional with variation reaches a minimum (maximum) value on , then there is
The extremum problem of a functional is to find a function to minimize (or maximize) the value of the functional .
For functionals that depend on multiple unknown functions
v [ y 1 ( x ), y 2 ( x ), ¼ , y n ( x )]
and a functional that depends on one or more functions of multiple variables
v [ z ( x 1 , x 2 ,
¼ , x n )]
or v [ z 1 ( x 1 , x 2 , ¼ , x n ), z 2 ( x 1 , x 2 , ¼ , x n ), ¼ , z n ( x 1 , x 2 , ¼ , x n )]
There are similar sayings .
2. The extremum of the functional with fixed boundary · Euler equation
Euler's equation is a necessary condition for functional extremum, but it is not sufficient . When dealing with practical functional extremum problems, the sufficient conditions are generally not considered, but the functional extremum value is indirectly judged from the nature of the actual problem The existence of , directly use Euler's equation to find the extreme value curve .
Assuming that F is second -order differentiable, the function y ( x ) is a function of class C2 and satisfies the boundary conditions
y ( x 0 )= y 0 , y ( x 1 )= y 1
The extreme value curve y ( x ) must satisfy the following differential equation (Eulerian equation)
or
This is a second-order differential equation whose general solution contains two arbitrary constants and is determined by two boundary conditions . It is therefore a two-point boundary value problem .
Integratable Types of 1 ° Euler Equations 
|
The integrand F _ |
Euler equation |
|
F does not depend on : |
|
|
F is linear with respect to : |
|
|
F only depends on : |
|
|
F depends on x and : |
|
|
F only depends on y and : |
|
Euler's Equation in 2 ° Polar Coordinates
|
functional _ |
Euler equation |
|
|
|
|
|
|
set function
Satisfy 2 n boundary conditions:
Euler's equation is
Assuming that the functions yi appearing in it are all continuous and the functions belong to the class C 2 , this system of second -order differential equations determines a family of integral curves with 2 n parameters in the space, and the 2 n parameters should be defined by the 2 n boundaries above. Conditions are determined .
Assuming that F is differentiable of order n + 2 , the function y ( x ) is of class C 2 n , and the boundary conditions are
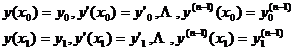
Euler's equation is
The general solution of this equation contains 2 n arbitrary constants, which can generally be determined by the 2 n boundary conditions above .
[ Extreme value of multiple integrals ]
1 ° functional 
Assuming that the function F is third-order differentiable, the function is second-order differentiable, and the value of the function on the boundary C of the region D is given, the Euler equation is
where . This is a second-order partial differential equation .
2 ° type functional 
Euler's equation is
in the formula
3 ° type functional 
Euler's equation is
in the formula 
[ Extremum of the parameterized functional ] Consider the form
The functional of , where the function under the integral sign does not contain an independent variable t explicitly , and is a first-order homogeneous function for and , namely
Then the form of the integral does not change regardless of any substitution of the parameter t . For any choice of the parameter t, the function and the system of equations should satisfy the two Euler equations :
These equations do not obviously contain the parameters themselves . But the two Euler equations are not independent, and one can be derived from the other . To find the extremum curve, just take one of the two Euler equations and add it to The equation that determines the parameter is integrated together . For example, if the arc length s of the curve is selected as the parameter, the equation that determines the parameter is .
3. The extremum of the functional of the movable boundary
1 ° If the two end points change on the curve and the sum respectively , the function that makes the functional reach its extreme value , except that it must satisfy the Euler equation
In addition, its endpoints must also satisfy the so-called transversal condition
2 ° If the curve where the two points are located is given in the form of an implicit function:
where there are continuous partial derivatives, and
, 
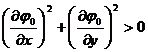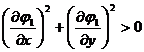
Then the transversal condition is
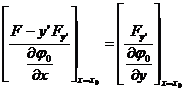
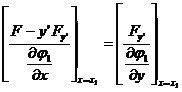
1 ° if both ends are on the curve
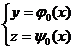and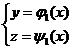 
changes up, then the function that makes the functional reach its extreme value , except that it must satisfy the Euler equation
In addition, its endpoints must also satisfy the transversal condition
2 ° if respectively on the surface
and 
changes upward, then the transversal condition is
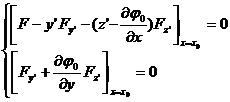
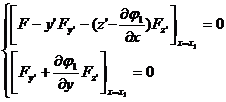
1 ° if the relationship is satisfied between 
Satisfaction relationship between
Then the function that makes the functional reach its extreme value , except that it must satisfy the Euler equation
In addition, its endpoints must also satisfy the transversal condition
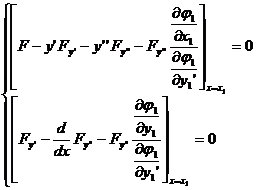
2 ° If the relational expression is satisfied and the relational expression is satisfied , then the transverse condition is 
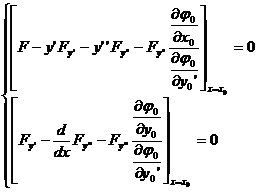
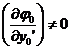
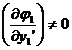
4. Conditional extreme value problem
[ Lagrange multiplier method ] Now consider the simplest conditional extreme value problem: find the sum of two functions , so that the functional
The extreme value is reached, and additional conditions are met
and boundary conditions for fixed endpoints
(The endpoints ( ) 
and ( ) 
should obviously satisfy additional conditions) .
The solution to this problem is similar to the Lagrange multiplier method for conditional extrema of multivariable functions introduced in Chapter 5 § 3. As an auxiliary function
where is an undetermined function of x , and the above conditional extremum problem is transformed into a functional of the integrand function
The unconditional extremum problem of
or
Eliminating Euler's equation and the constraint equation together and a function to be solved (such as z ), then a second-order differential equation containing a function is obtained, and the two arbitrary constants of its integral are determined by the two boundary conditions .
[ Isoweek problem ] In making points
equal to the known constant a and satisfy the boundary conditions
Among all the curves of , determine a curve such that the functional
Reach the extreme value . This problem is called the isoperimetric problem . The solution is as follows:
Construct helper function
where is an undetermined constant, the above conditional extremum problem is transformed into a functional with H as the integrand
The unconditional extremum problem of
The general integral of this equation contains three arbitrary constants, namely the two integral constants and the constant . These constants are determined by the two boundary conditions and the isoperimetric condition . But note that only if the resulting curve is not the integral in the isoperimetric condition
The solution to the isoperimetric problem is the extreme value curve of .
[ Optimal Control of Continuous Dynamic System ] Let the state equation of the control system be
(1)
where x is an n -dimensional state vector, m is an r -dimensional control vector, f is a differentiable n -dimensional vector function, and the initial condition is
(2)
The performance index of the system is
(3)
The purpose of optimal control is to determine the control vector under the constraints (1), (2) , so that the performance index (3) takes the minimum value . This is a conditional extreme value problem .
as a helper function
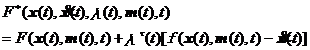
where is the Lagrange multiplier factor, which is an n -dimensional column vector . The problem is reduced to a functional
The unconditional extremum problem of , thus obtains , , and the necessary conditions to be satisfied for the functional to take an extremum:
(i)
( governing equation )
(ii)
( Equation of State )
(iii)
( Eulerian equation )
(iv)
( transversal condition )
where is an arbitrary vector function defined on the interval [ ] . In this way, the problem is reduced to a two-point boundary value problem for solving ordinary differential equations. The analytical solution of this problem exists only in special cases. Differential equations are usually nonlinear and are generally solved by the "trial and error" method .
It shows that when the optimal design of the control system is carried out by the variational method, there is generally no restriction on the control vector , that is, only the control domain or open set to which the control vector belongs is considered , but in practical problems, U is often a bounded set, And the value of optimal control will appear on the boundary of U , which is another difficulty in addition to the two-point boundary value problem when using the variational method for optimal control of the control system . 
5. Direct Approaches to Variational Problems
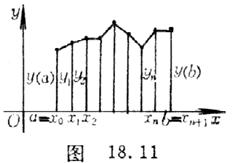
[ Eulerian Finite Difference Method ] Consider the functional
The extreme value of , the boundary condition is
The steps are as follows:
(1)
Divide the integral interval into n + 1 equal parts (Figure 18.11 ) , and the dividing point is
again . this time
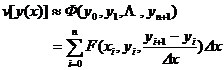
in the formula
(2)
Choose to make the function reach the extreme value, that is, by the system of equations
to determine . If it is difficult to determine from this system of equations , the method of § 2, § 3 of this chapter can also be used . The obtained polyline can then be used to represent the approximate solution of the variational problem .
The finer the interval [ a , b ] is divided, the more accurate the approximate solution will be .
[ Ritz Method ] Consider the functional
The extreme value of , the boundary condition is
The steps are as follows:
(1)
Choose an appropriate sequence of functions (called coordinate functions):
Constructor
where is an undetermined constant . Substituting the approximation of , into the expression of the functional , then
(2)
Select to make the function reach the extreme value, that is, by the system of equations
to determine . If it is difficult to determine from this system of equations , the method of § 2, § 3 of this chapter can also be used . Then an approximate solution to the variational problem can be obtained .
When n is larger, the approximate solution obtained is more accurate .
The Ritz method also works for functionals and functionals that depend on multiple functions .
Example to find functional
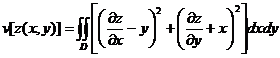
, where the integration domain D is an ellipse .
The solution takes only one coordinate function xy , then we get
,
From this time
get
The approximate solution to the extreme value problem is
[ Kantrovich's method ] Consider the functional
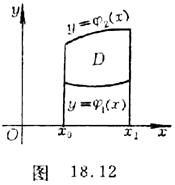
(1)
The extreme value of , which spreads over the region D bounded by two curved lines and two straight lines ( Fig . 18.12 ). The value z ( x , y ) of the function set on the boundary of the region D has been given . The steps are as follows :
(1)
Select the coordinate function sequence:
Constructor
where is the undetermined function . The approximate expression of z ( x ,
y )
Substitute into (1) to get
which is
(2)
Select the function to make the functional reach the extreme value, that is, by Euler's equation
to determine . The choice of any constant is to satisfy the given boundary conditions on the straight line sum . Then the approximate solution of the variational problem can be obtained .
Kontrovic's method is also applicable to other forms of functionals .
Description In general, with the same coordinate function and the same number of terms m , the Kantrovich method is more accurate than the Ritz method . Because the function class with variables as coefficients 
Compared to function classes with constants as coefficients
more expansive .
