§ 5 Elasticity Theory and Finite Element Solution
The finite element method is very effective for solving small deformation problems of elastic bodies . This is because the deformation energy and the external force potential energy or the total potential energy can be expressed as a quadratic functional with a uniform form . Due to the formulation of elastic mechanics problems , especially the boundary conditions Therefore , in this section, in addition to introducing the basic relational expressions related to various problems and B, D, etc. in § 1 , it also focuses on analyzing and discussing various problems . The role of boundary conditions in relevant variational problems, and the equivalence of various variational problems and definite solutions of differential equations is discussed.
1.
The three-dimensional elastic problem
This section discusses the internal force and deformation of the elastic body in the Cartesian coordinate system ( x , y , z ) . In order to simplify the discussion , it is assumed that the elastic body is simply connected , uniform and isotropic, and if necessary, the usual vector Notation to highlight its mechanical significance .
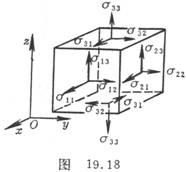 [ Stress and Balance Equation ] Under the action of external force, temperature difference, etc., the elastic body will generate internal force between each part, indicating that the size of the internal force is the strength of the force on the acting surface or the force per unit area , that is, the so-called stress . For elasticity At a point P in the body, a micro-hexahedron can be made in its vicinity, and its edges are parallel to the coordinate axis. Three of the six faces of the hexahedron have the same direction as the x - axis, y - axis or z -axis respectively (the other three are opposite to the coordinate axis) , which can be called x , y , z coordinate planes respectively ( Or the 1st , 2nd , and 3rd coordinate planes ). Let the stresses acting on the x , y , and z coordinate planes be represented respectively , and the three components to be recorded are ( the signs of the stresses on the remaining three planes are reversed .
[ Stress and Balance Equation ] Under the action of external force, temperature difference, etc., the elastic body will generate internal force between each part, indicating that the size of the internal force is the strength of the force on the acting surface or the force per unit area , that is, the so-called stress . For elasticity At a point P in the body, a micro-hexahedron can be made in its vicinity, and its edges are parallel to the coordinate axis. Three of the six faces of the hexahedron have the same direction as the x - axis, y - axis or z -axis respectively (the other three are opposite to the coordinate axis) , which can be called x , y , z coordinate planes respectively ( Or the 1st , 2nd , and 3rd coordinate planes ). Let the stresses acting on the x , y , and z coordinate planes be represented respectively , and the three components to be recorded are ( the signs of the stresses on the remaining three planes are reversed .![]()
![]()
![]() For example , the components shown on Figure 19.18 are all positive ), these nine components ( i , j = 1 , 2 , 3 ) form a tensor called the stress tensor .
For example , the components shown on Figure 19.18 are all positive ), these nine components ( i , j = 1 , 2 , 3 ) form a tensor called the stress tensor .![]()
It can be seen from the figure that the component represents the normal stress on the i -th coordinate plane ( positive in tension and negative in compression ); and the component represents the two components of the shear stress along the i -th coordinate plane ( the one that makes the torsion angle an acute angle) is positive ). The law of mutual shear stress can be obtained from the balance of the microelement hexahedral moment , that is,![]()
![]()
![]() = ( )
= ( )![]()
![]()
Therefore, the stress tensor is symmetric , and only six of its components are independent . In the finite element solution method , the six components are generally arranged into a column vector in the following order , and recorded as
![]()
Assume that an arbitrary inclined plane passes through the point P , and the cosine of its normal line n is ( ), then the three components of the stress acting on the inclined plane can be obtained by using the equilibrium condition of the tetrahedron enclosed by the three-coordinate plane![]()
![]()
![]() ( j =1 ,2,3 )
( j =1 ,2,3 )
Then the projection on the line whose direction cosine is ( ) , that is, its component is![]()
![]()
![]()
This shows that the stress state at a point is completely determined by the six stress components { s } at that point . For example , the normal stress acting on the above slope is
![]()
And along the direction of the shear stress of the inclined plane , the magnitude is equal to![]()
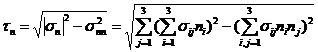
Conversely , for the inclined plane called the stress principal surface of point P , the corresponding normal is called the principal axis of stress at point P , and its normal stress is called the principal stress of point P. It can be proved that at any point in the elastic body , there must be Three principal stresses that are orthogonal to each other , and the largest ( smaller ) one is the maximum ( small ) normal stress at the point . The sum of the three normal stresses![]()
![]()
![]()
Called the volume stress , it is an invariant under the coordinate transformation , so it is equal to the sum of the three principal stresses .
Let , represent the physical force ( external force per unit volume ) acting on the point P , and the balance equation of the force can be derived by integrating the volume elements or analyzing the mean value![]()
![]() ( i =1 ,2,3 ) (26)
( i =1 ,2,3 ) (26)
 [ Strain and Geometric Equation ] Any point P ( x , y , z ) in the elastic body moves to its displacement function after a small deformation as
[ Strain and Geometric Equation ] Any point P ( x , y , z ) in the elastic body moves to its displacement function after a small deformation as![]()
![]()
in the formula
![]()
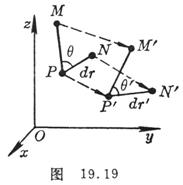
They are trace functions of ( x , y , z ) , assuming that there is a tiny line segment PN = dr whose direction cosine is ( ), after small deformation becomes , the normal strain along this direction is defined as unit elongation , namely![]()
![]()
![]()
![]()
It is not difficult to obtain from the expressions of displacement with dr before and after deformation![]()
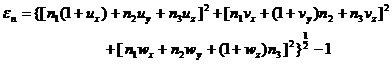
Expanding the radicals on the right-hand side and omitting higher-order infinitesimals ( ie, higher-order terms of the displacement derivative ), we get
![]()
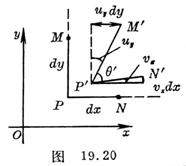 Let the cosine of the direction of another line segment PM be ( ), the angle before deformation , then
Let the cosine of the direction of another line segment PM be ( ), the angle before deformation , then![]()
![]()
![]() ( 27 )
( 27 )
Set the angle after deformation ( Fig . 19.19 ), then![]()
![]()
According to the changes in the size and direction of the two line segments before and after the deformation , it is not difficult to draw
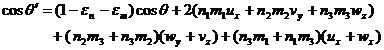
![]() ( 28 )
( 28 )
Comparing with ( 27 ) and ( 28 ), we can know that as long as the following six derivative values are given at point P :
 ( 29 )
( 29 )
The deformation state adjacent to point P can be completely determined . It represents the normal strain along the ith coordinate axis , and represents the right angle change between the ith and j coordinate directions after small deformation , which is the so-called shear strain ( as shown in Figure 19.20 , After deformation, the acute angle is positive , and the obtuse angle is negative . These six quantities are called strain components , which are recorded as![]()
![]()
![]()
![]()
It can also be proved that at any point in the elastic body , there must be mutually orthogonal strain principal axes , and the intersection angle of the three axes remains at right angles after deformation , that is, the shear strain is zero ; the normal strain of the three principal axes is called the principal strain , and the largest ( smallest ) One is the maximum ( small ) normal strain at that point . The sum of the three normal strains
![]()
is called volumetric strain , which is also an invariant , and represents the amount of change per unit volume in the microelement . For an isotropic body, the direction of the principal axis of stress and the principal axis of strain are still the same . The deformation energy density described in § 1
![]()
It is derived by transforming the coordinate system to a common principal axis direction and applying Hooke's law .
The relational formula ( 29 ) is called a geometric equation , and its matrix form is
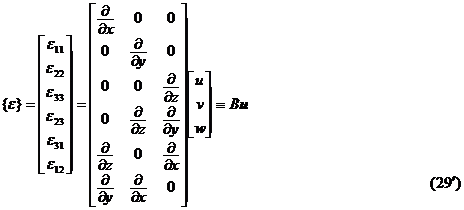
[ Physical equation and elastic coefficient ] The small deformation experiment of simple tension and compression on the rod proves that a single axial ( taken as the x - axis ) force will not cause shear strain , and the relationship between the normal pressure and the normal strain has the following linearity relation![]()
![]()
![]() or
or![]()
If the elongation along the x direction is taken into account along with the lateral contraction , the normal strain along the y and z directions is generated
![]() or
or![]()
This is Hooke's law , where the coefficients E and v are called elastic modulus and Poisson's ratio , respectively . From Hooke's law, the general relationship between strain and stress can be deduced , the so-called physical equation
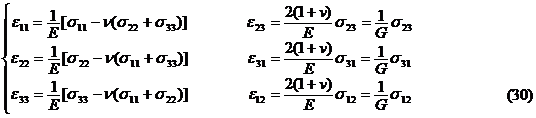
is called the shear modulus of elasticity .![]()
The relationship between stress and strain is obtained by inverting ( 30 )
![]()
Or written in matrix form :

where G is called the Lamé coefficient , and e is the volumetric strain . It is proportional to the volumetric stress Θ :![]()
![]() or
or ![]()
The proportionality constant is called the bulk modulus of elasticity .![]()
[ Boundary condition ] Boundary Ω ' of elastic body Ω is subjected to surface force
![]()
There are three ways : fixed support , load support and elastic support . Assuming that the parts of Ω ' accepting these three kinds of supports are denoted as and respectively , the boundary conditions can be expressed as![]()
![]()
1° Geometric Constraints : Given the displacement above , i.e.![]()
![]()
2°
surface force balance condition : a given load on the upper surface is the surface force q , ( ) represents the cosine of the outer normal line of any area element on the upper surface . Since the stress needs to be balanced with the surface force , the condition can be obtained from ( 27 ) as ![]()
![]()
![]()
![]()
3°
coupling equilibrium condition : the upper elastic body is coupled with another elastic structure , the displacement on these coupled boundaries is neither constrained nor completely free , but accepts its displacement deviation ( relative to a given displacement value ) as a result. is proportional to the elastic reaction force . Its three components per unit area can be expressed as ![]()
![]()
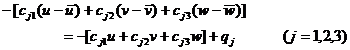
Here the elastic support coefficient matrix C = ( ) ![]() is positive definite , and can be regarded as a given surface force . Likewise , this reaction force should be balanced by the stress on it . Then its condition can be written as
is positive definite , and can be regarded as a given surface force . Likewise , this reaction force should be balanced by the stress on it . Then its condition can be written as![]()
![]()
![]()
[ External force potential energy and its calculation formula ] In the elastic body and its boundary , all the parts of the given external force that do work due to deformation must be accumulated , and the minus sign can be regarded as the potential energy of the elastic body relative to the external force system , that is The so-called external force potential energy - F ( u ) . For example, in the elastic body, in addition to the physical force f, there may also be part of the concentrated surface force, line force and point force, the inner product of these forces and the displacement of the part is the work they do , and therefore must be counted. On the boundary, except for the geometrically constrained part, the external forces applied to the rest , including surface force, line force and point force, all contribute to the external force potential energy , and formulas should also be introduced . In order to simplify the calculation formula , the same formula (1)~ (7) Only the physical force f is listed the same as the face force q , and the situation of concentration is not considered here .
Assuming that geometric constraints, surface force and elastic reaction force are respectively applied to the boundary part of the elastic body Ω , and the elastic reaction force , the work done by the external force due to the deformation is equal to![]()
![]()
![]()
![]()
take inner product notation
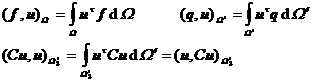
In the formula, C = ( ) ![]() represents the positive definite elastic coupling coefficient matrix , and - C u is the elastic reaction force generated by the displacement u . Therefore , the work W by the external force can be abbreviated as
represents the positive definite elastic coupling coefficient matrix , and - C u is the elastic reaction force generated by the displacement u . Therefore , the work W by the external force can be abbreviated as
![]()
The third integral on the right side of the above formula is the external work generated by the boundary deformation, which is a quadratic functional of u , so it can be regarded as a part of the deformation energy of the elastic body after changing the number, so the total potential energy can be written as
![]() ( 32 )
( 32 )
where the deformation energy is represented , and -F ( u ) represents the external force potential energy , namely![]()
![]()
![]()
2. Two
-dimensional elasticity problem
This paragraph only discusses the three common problems of plane stress, plane strain and sheet bending in the Cartesian coordinate system. For a tensile thin plate , it can be considered that the normal stress and shear stress along the thickness direction of the plate are equal to zero . Generally, the mid-plane of the thin plate is taken as the xy plane , and it can be assumed that
![]()
There are only three stress components along the xy plane : and , and they are independent of the coordinate z . This is the plane stress problem . Conversely , analyze the deformation of a fairly long prism ( eg, a gravity dam ) when subjected to a constant external force along its length , it can be considered that each point has only a displacement parallel to its cross section ( taken as the xy plane ) ( ie w = 0 ), and its displacement is constant along the length ( ie u , v have nothing to do with z ), from the geometric equation we can see![]()
![]()
![]()
There are only sums along the xy plane , and independent of z , which is a plane strain problem .![]()
![]()
Analyzing the bending of the thin plate caused by the lateral load , it can be considered that the points on the midplane do not have longitudinal displacement , that is , when z = 0 , u = v = 0 , and the lateral displacement w of the plate does not change along the thickness , that is, w =
w ( x , y ) has nothing to do with z . In addition , although the normal stress and shear stress along the plate thickness direction are not equal to zero , they are much smaller than other stress components , and the influence on the deformation can be ignored , so there is the same problem as the plane stress problem. physical equations .
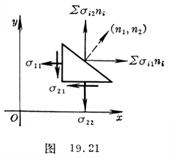 [ Plane stress problem ] The stress component acting on the section with the cosine of the normal direction ( ) is
[ Plane stress problem ] The stress component acting on the section with the cosine of the normal direction ( ) is![]()
![]()
![]()
Equilibrium equation for 1° force

The 2°
boundary condition assumes that the boundary receives fixed support , and the parts of load support and elastic support are respectively denoted as , then the boundary conditions can be expressed as ![]()
![]()
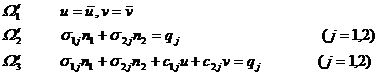
3°
geometric equation
![]()
4°
Physical Equations
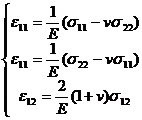 or
or 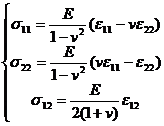
5°
Matrix B and D
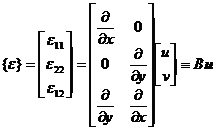
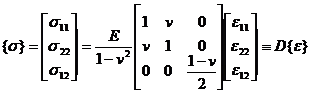
Note that from the physical equation ( 30 ) it is also deduced
![]()
It is the amount of change per unit plate thickness .
The expression of the total potential energy at 6° is exactly the same as ( 32 ) in form , but it should be noted that this is a two-dimensional case .
[ Plane strain problem ] The equilibrium equation of force , boundary conditions, geometric equation ( thus matrix B ) and the expression of total potential energy are the same as for plane stress problem . From and (30) , its physical equation can be deduced![]()
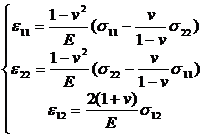 or
or
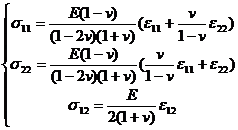
Comparing with the physical equation of the plane stress problem, it can be seen that the physical equation of the plane strain problem can be obtained by changing E and v to The problem is consistent . The corresponding matrix D can be written as![]()
![]()
![]()
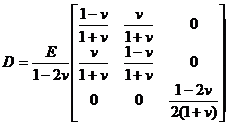
Note that from the physical equation ( 30 ) the longitudinal positive pressure is also derived
![]()
It is the surface force that should be applied to both ends of the prism to make it unstrained in the longitudinal direction .
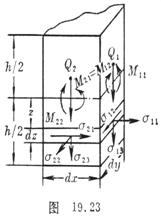
[ Thin plate bending problem ] The small deformation of the thin plate can be completely represented by the deflection ( that is, the displacement along the z direction ) of the mid- plane ( taken as the xy coordinate plane ) w =
w ( x , y ) . The elastic surface z = w ( x , y ) after z = 0 is deformed . At this time, the normal line segment of the mid-plane point ( x , y , 0) of the plate is assumed to be only rigidly displaced to the normal line segment of the surface ( Figure 19.22 right ) , its direction number is
![]() .
.
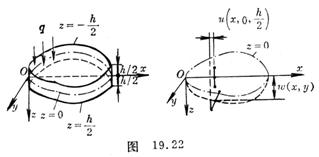
Therefore , the displacement component of any point ( x , y , z ) in the thin plate ( ![]() , h is the thickness of the plate ) can be written as
, h is the thickness of the plate ) can be written as
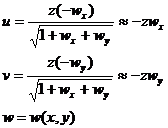
The trace higher-order terms are omitted here . Similarly , we can record the first-order approximation of the three curvature components of the deformed surface as![]()
![]()
and the geometric equations are written as
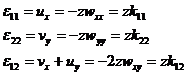
The main stress components in the physical equation can then be written as
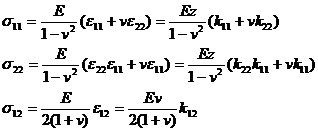
These components appear paired with the strain component above in the integral of the deformation energy and have a common factor of![]()
![]()
![]()
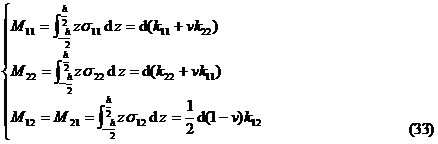
in the formula
![]()
It is called the bending rigidity of the plate, and is the bending moment and torque on the single-width section orthogonal to the x and y axes.![]()
![]()
The relationship between these internal forces and stresses is clearly as follows :
![]()
Therefore, it is called generalized stress and generalized strain , and ( 33 ) is called generalized Hooke's law .![]()
![]()
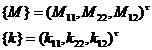
Then the deformation energy can be written as
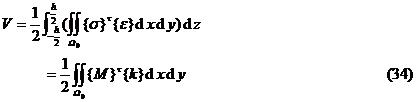
 where represents the area of the mid-surface of the thin plate . Since the undetermined function has only the displacement component w ( x, y ) , we can make
where represents the area of the mid-surface of the thin plate . Since the undetermined function has only the displacement component w ( x, y ) , we can make![]()
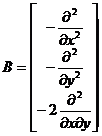
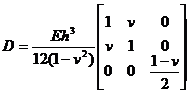
And substituting { k } = B w, { M } = D { k } into ( 34 ), we get
![]()
The second-order partial derivative of the displacement function w appears in the integral formula, which is essentially different from the plane problem where only the first-order partial derivative of the displacement functions u and v occurs .
[ Total potential energy of elastic surface and plate ]
The differential equation of the 1°
elastic surface not only has a great influence on the deformation in the stress component , but also the bending moment and torque generated by them are the basic internal forces in transferring the load to the boundary . However, the internal force directly balanced with the external force However, it is the rest of the components . Therefore , in order to obtain the shape of the elastic surface , the relationship between each stress component ( j= 1 , 2 , 3) and w should also be considered .
![]()
![]()
Since the body force of the thin plate is negligible , according to the stress balance equation ( 26 ) and the boundary conditions of the upper and lower plates , the integral of z can be obtained![]()
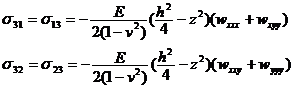
Substitute into the third equation of ( 26 ) to find out . Generally speaking , the lower plate surface is suspended in the air, that is, there is no surface force , so according to its boundary conditions : through the integration of z , we can get![]()
![]()
![]()
Finally, according to the boundary conditions of the load intensity q ( positive downward ) applied to the upper plate surface , and using the notation of the Laplace operator , we can get![]()
![]()
This is the fourth-order differential equation of the elastic surface , where d is the bending stiffness of the plate . To solve for w , the boundary conditions along the edge ( section ) of the thin plate also need to be considered .
In order to unify the expression of the boundary conditions of the 2° plate, it is assumed that the shear forces generated by the single-width section perpendicular to the x and y axes are respectively![]()
![]()
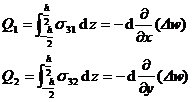 (35)
(35)
Secondly , draw the tangent direction s and the outer normal direction n on the boundary of the mid-plane area , so that the n , s and z axes form a right-hand local coordinate system ( refer to Figure 19.24 ) , and set the direction cosines of s and n as .![]()
![]()
![]()
Contrasting (33), (35) obviously have equilibrium equations :
![]()
If the shear force acting on a single-width edge section with an outer normal of n is expressed , the equilibrium equation is obtained :![]()
![]()
in the formula
![]()
They represent the single-width bending moment and torque generated by the normal stress and shear stress acting on the edge section, respectively .![]()
![]()
The various boundary conditions of thin plates can basically be divided into the following three categories :
(i)
Geometric constraints
(a)
The deflection of a given section boundary : . For example, fixed edges and simply supported edges must be given w= 0 . ![]()
(b)
The angle of rotation of a given edge section about the tangent s . For example , in addition to w= 0 , the fixed edge should also be given = 0 . ![]()
![]()
(ii)
Load bearing
(a) Given a lateral linear force load p on a single-width boundary , it is balanced by the shear force on the edge section and the shear force generated by the tangential rate of change of torque , i.e. ![]()
![]() ( p is positive towards the z direction )
( p is positive towards the z direction )
For example, in the free edge part p = 0 , the left-hand side of the above formula includes the third-order partial derivative of w .
(b) The moment load around the tangential direction s is given for a single-width edge section . For example, the same as p in the free edge part , . ![]()
![]()
![]()
(iii) Elastic support
(a) In addition to the lateral linear load, it also bears an elastic reaction force - cw proportional to the deflection , where c > 0 is the elastic coupling coefficient, and its condition can be written as
![]()
(b) In addition to the moment load, an elastic reaction moment proportional to the rotation angle of the section about the tangential direction is subjected , where > 0 is also the elastic coupling coefficient. Its condition can be written as ![]()
![]()
![]()
Note that two conditions given on the same boundary cannot be of the same type ( a ) or ( b ).
The two conditions given by the expression of 3° total potential energy assume that all elastic supports are on the boundary of the mid-plane region, and the equilibrium condition is ![]()
![]()
![]() ( c ,
( c , ![]() > 0)
> 0)
The expressions of deformation energy and external force potential energy can be written as
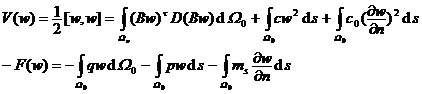
If the deflection and the rotation angle about the tangential direction s are respectively given on part of the boundary , the integral line segments related to these geometric constraints should be removed respectively in the latter two-line integral of the expression. So the total potential energy can be written as![]()
![]()
![]()
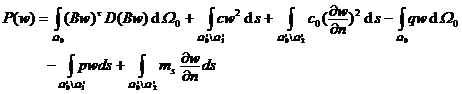
When other parts are changed to load supports, as long as the c or of this part is taken as zero, the expression remains the same.![]()
3. One-dimensional elasticity problem
This paragraph only discusses the torsion problem of the cylinder, because it uses the torsion rate as the generalized strain . Other problems such as expansion and contraction of rods and bending of beams can be regarded as simplifications of two-dimensional problems and have little to do with the finite element method . Slightly .
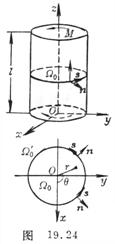 [ Twisting of the cylinder ] The radius of the cylinder is R , the central axis of the cylinder is taken as the z - axis , the two ends are z = 0 , z = l , and the body force is not counted . First, consider that only the opposite couple moments M are applied to the cross-sections at both ends ( Fig. 19 ). . 24 ) . It can generally be assumed that only the torsional shear stress along each cross section is generated and the remaining components
[ Twisting of the cylinder ] The radius of the cylinder is R , the central axis of the cylinder is taken as the z - axis , the two ends are z = 0 , z = l , and the body force is not counted . First, consider that only the opposite couple moments M are applied to the cross-sections at both ends ( Fig. 19 ). . 24 ) . It can generally be assumed that only the torsional shear stress along each cross section is generated and the remaining components
![]() ( i =1 ,2,3 )
( i =1 ,2,3 )
It can be seen from the physical equation that it is also a pure shear deformation. Taking polar coordinates on the circular section also constitutes the torsion of the cylinder in the right-handed coordinate system ( Figure 19.24) , and it is further assumed that![]()
(i)
, that is, each circular section has no axial displacement;![]()
(ii) Any circular section will make a slight rotation about the center of the circle.
Let the rotation angle be ω ( z ), then ω ( z ) -ω (0) represents the torsion angle relative to the end face z section z = 0 , and ω ( l ) -ω (0) is the total torsion angle of the cylinder. Generally, ω (0)=0 can be set , that is, one end is fixed.
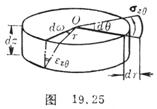
Considering the torus of radius r between z and z + dz section , it is not difficult to see that the change in right angle due to the relative torsion angle dω is the shear strain
![]()
It is the result of shear stress on the torus in the direction q (or perpendicular to the radius r ) , according to Hooke's law ![]()
![]()
According to the symmetry of the shear stress, the torque along the z section can be obtained
![]()
where is the moment of inertia of the section about the central axis. So the deformation energy can be written as![]()
![]()
Therefore, the torque and torsion rate of the cylindrical torsion problem can be regarded as generalized shear stress and shear strain, respectively. The coefficient is called the torsional stiffness of the column. For this problem, in §1 , B is a differential operator , D is , and the undetermined function is the generalized displacement or torsion angle ω ( z ) .![]()
![]()
![]()
![]()
![]()
extended to the general case. If a distributed load, i.e. torsion , is applied per unit length along the column, the equilibrium equation can be written as![]()
![]()
The boundary conditions also have three support forms:
(i)
Geometric constraints give a twist angle ω to the column end section . E.g ![]()
(ii) The load bearing applies a certain torsion to the column end section. E.g
![]() or
or![]()
(iii) The elastic support at the column end section gives an elastic reaction moment proportional to the deviation of the torsion angle. E.g
![]() or
or![]()
where is the elastic coupling coefficient.![]()
Since the expression of the total potential energy does not count the physical force, in the case of elastic support, the deformation energy and the external force potential energy can respectively represent the functional form of ω ( z ) :
If a certain end is a load support, this end can be selected , and the expression remains the same; if a certain end (such as z = 0 ) is given a torsion angle , the term containing the end point z = 0 in the above two equations must be removed, and the total potential energy The expression can be written as![]()
![]()
![]()
[ torsion of cylinder ] is the same as torsion of cylinder, assuming that the body force and the surface force of the side are not counted, and only a couple moment M is applied at both ends , the displacement component of the torque can be written as![]()
![]()
where is the torsion rate, called the warpage function.![]()
![]()
geometric equation
![]()
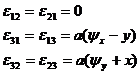
physical equation
![]()
![]()
The equilibrium equation can be obtained from ![]()
![]()
where is the cylinder section.![]()
The direction cosine of the outer normal line of the boundary set by the boundary condition is , since the side surface of the column is not subject to surface force, the boundary condition can be obtained from the physical equation ![]()
![]()
![]()
![]()
According to , it can be known from the equilibrium equation and boundary conditions that its general solution is in the form ( for an arbitrary constant). a can be determined by the moment balance condition of the section at both ends, such as the torque from the end face z = l![]()
![]()
![]()
![]()
torsion rate
![]()
Therefore, it can be regarded as displacement, and the problem boils down to finding the total potential energy![]()
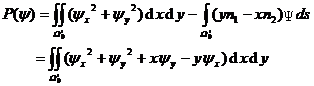
solution to the extreme value.
4. Problems related to finite element solution
When discussing space and plane problems , for the sake of simplification , the coordinates ( x , y , z ) are replaced by ( ), ![]() u still represents the displacement column vector , and its three components are replaced by ( ) (
u still represents the displacement column vector , and its three components are replaced by ( ) ( ![]() u , v, w ); for the physical force f Equal loads are still represented by ( ) ; for integrals , except for formula calculus , generally only an integral sign is used to represent them .
u , v, w ); for the physical force f Equal loads are still represented by ( ) ; for integrals , except for formula calculus , generally only an integral sign is used to represent them .![]()
[ Positive Determination of Deformation Energy and Rigid Displacement ] The elastic coefficient matrix D is positive definite , which can be deduced from the deformation energy V = 0 , that is , it is positive definite for strain , but degenerates to non-negative for displacement , that is, it cannot be deduced , because the elastic body still has a strain-free displacement, that is, a rigid displacement .![]()
![]()
![]()
![]()
1°
general space problem Let the component of the curl rot u of the displacement vector field u be
![]()
The relationship between it and the displacement component and the strain component is:
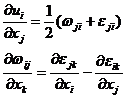
![]()
![]()
Therefore , under the assumption of small deformation , the strain represents that the entire elastic body can perform a small rotation in addition to a small displacement, and its rigid displacement can be written as![]()
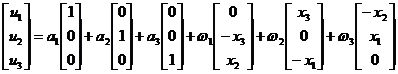
where is the component of translation and the angle of rotation around the three-coordinate axis , and they are all arbitrary tiny constants . In short , there are six degrees of freedom in the tiny rigid displacement of the elastic body without strain .![]()
![]()
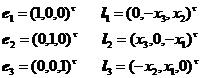
The above formula can be abbreviated as
![]()
where is the unit vector of the i -th coordinate axis , which is the arm vector around the i -th coordinate axis . So![]()
![]()
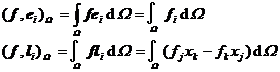 ( i =1 ,2,3 )
( i =1 ,2,3 ) ![]()
respectively represent the components of the resultant force and moment of the distributed body force f on the elastic body along the i -th coordinate axis . There are similar results for the distributed loads such as the surface force q .
The 2°
plane stress and strain problem is simplified because the rigid displacement is ![]()
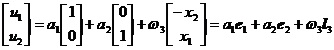
Its degree of freedom is equal to 3 . The inner product of the distributed load and , has a similar definition and meaning .![]()
![]()
3°
thin plate bending problem Since the displacement component is only deflection , the rigid displacement can be written as
![]() ( ie )
( ie )![]()
Its degrees of freedom are equal to 3 . Inner product
![]()
respectively represent the resultant force of the distributed load q along the mid-plane and the resultant moment around the axis .![]()
According to the assumption of w = 0 and the generalized shear strain , that is, the torsion rate of the 4° cylinder torsion problem , the rigid displacement without strain can be obtained . The corresponding arm vector is . At this time , the displacement can also be written as
![]()
![]()
![]()
![]() ( ie
)
( ie
)![]()
Its degree of freedom is equal to 1 . Given a distributed load shear force Q on the end face ( its distribution , strictly speaking , should be the same as the shear stress ), the inner product is the resultant moment M along the end face .![]()
![]()
[ Solvability of variational problems ] Only general space problems , thin plate bending problems and cylindrical torsion problems are discussed here , and other problems are analogous .
For general space problems , consider the case of boundary pure load support first . It can be seen from § 1 that solving the displacement function u makes the total potential energy of the elastic body reach a minimum value , namely
![]()
The variational problem of can be reduced to solving the variational equation
![]() ( to everything )
( to everything )![]()
, where the variational displacement of the displacement u is called virtual displacement , and the integral
![]()
Called the virtual work functional , it is a bilinear functional of the displacement u and the virtual displacement .![]()
It has been pointed out above that the deformation energy can only be obtained for any rigid virtual displacement . On the contrary , for all non-rigid virtual displacements . . Therefore, using the equation![]()
![]()
![]()
![]()
![]()
It can be shown that the necessary and sufficient conditions for the solution of the variational problem are
![]() ( for all rigid virtual displacements )
( for all rigid virtual displacements )![]()
Since the degree of freedom of rigid displacement is 6 , ![]() it can be divided into 6 conditions
it can be divided into 6 conditions
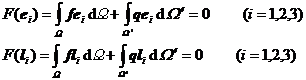
This shows that the sufficient and necessary condition for the elastic body to reach equilibrium under pure load support is that the resultant force and the resultant moment generated by the external force on the entire elastic body are equal to zero .
Conversely , if the variational problem has a solution , the sum of displacement and any tiny rigid displacement + is also its solution , which shows that the equilibrium state of the elastic body can differ by a tiny rigid displacement , with 6 degrees of freedom . In other words , the general form of the solution can be written as![]()
![]()
![]()
![]()
![]()
![]()
If there is still a part of the boundary that is geometrically constrained or elastically supported , the number or degrees of freedom of the necessary and sufficient conditions for the solution will be reduced accordingly . The solution exists and is unique . For example, when u is given a displacement value on a partial boundary , the variational equation is changed to![]()
![]()
![]() (for )
(for )![]()
As long as three points that are not collinear are included , the condition excludes all rigid virtual displacements , and the number of necessary and sufficient conditions for the existence of the solution is equal to zero . If elastic support is applied to part of the boundary , the deformation energy![]()
![]()
![]()
![]()
And the positive definiteness of the two integrals can be obtained
![]()
And the positive definiteness of C is deduced . Therefore , as long as three points that are not collinear are included , then the deformation energy is positive definite to the displacement u , and the solution of the problem exists and is unique .![]()
![]()
![]()
The 2°
thin plate bending problem considers the case of pure load support , and its deformation energy and external force potential energy can be expressed as generalized strain as follows
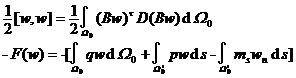
variational problem
![]()
It boils down to solving a variational equation
![]() ( for all virtual displacements )
( for all virtual displacements )![]()
Similarly [ , ]=0 can only get generalized strain , rigid virtual displacement can be expressed as![]()
![]()
![]()
![]()
![]()
Its degrees of freedom are equal to 3 , and the necessary and sufficient conditions for the solution of the variational equation are
![]() ( for all rigid virtual displacements )
( for all rigid virtual displacements )![]()
Since the above formula can be divided into three conditions :![]()
![]()
![]()
![]()
The former condition is that the external force along the thickness direction of the plate should be balanced so that the plate does not move ; the latter two conditions respectively indicate that the moment about the x and y axis directions generated by the external force on the plate should be balanced so that the plate does not rotate . In these Under the condition that the equilibrium state of the plate is not unique but has 3 degrees of freedom , that is, the solution of the problem can be written as
![]()
If there is still a part of the boundary that is geometrically constrained or elastically supported , the number of solvable sufficient and necessary conditions or degrees of freedom will be reduced or equal to zero . For example , as long as there are three non-collinear points given deflection , or a given point The deflection and two rotation angles around different directions make it impossible for the plate to have a small rigid displacement , and the solution to the problem exists and is unique . Applying elastic reaction force or reaction moment to part of the boundary will also improve the positive determinacy of the deformation energy . For example, in Given an elastic reaction force - cw and reaction moment on a part of the boundary , from Bw o 0 and , even just one point reduces two degrees of freedom , if there are two different outer normal directions , the degree of freedom is zero . At this time [ w , w ] is positive definite for w , and the solution to the problem also exists and is unique .![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. The cylindrical torsion problem considers the case of pure load support , and its deformation energy and external force potential energy can be expressed as a generalized displacement ( ie torsion angle ) ω as follows
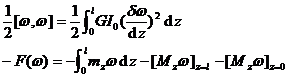
variational problem
![]()
It boils down to solving a variational equation
![]() ( to everything )
( to everything )![]()
Similarly , [ , ]=0 can only give the torsion rate . The rigid ( generalized ) virtual displacement can be expressed as , its degree of freedom is equal to 1. The sufficient and necessary condition for the solution of the variational equation is![]()
![]()
![]()
![]()
![]() ( for all twist angles around the z -axis )
( for all twist angles around the z -axis )![]()
This means that the torques along the entire cylinder are balanced . Under this condition , the equilibrium states of the cylinders can differ by a small torsion angle , i.e. the solution can be written as
![]()
As long as one end is geometrically constrained , the degrees of freedom disappear ; if one end ( for example , z = l ) is elastically supported , the corresponding deformation energy ( for example ) is positive definite . For these cases , the solution to the problem exists and is unique![]()
![]()
[ Equivalence of Variational Problem and Definite Solution of Differential Equation ] The equilibrium equation of the internal force of an elastic body is derived from the mean value analysis of its elements in the equilibrium state ; similarly , its boundary condition is also the internal force on the boundary element It is the embodiment of achieving balance with external force . Therefore , the problem of definite solutions of various differential equations in elastic mechanics is to find the equilibrium state of internal and external forces caused by continuous deformation of the elastic body . The variational problem is in the form of the energy of the entire elastic body. To express this equilibrium state , whether it is a deformation energy functional or a virtual work functional , its essence is the same . Here we also point out its equivalence with the problem of definite solutions of differential equations . The following is still the general space problem, thin plate The bending problem and the cylindrical torsion problem are briefly introduced as examples .
1°
Balance equation of force for general space problem
![]()
It can be regarded as a set of second-order differential equations about the displacement component ( ) ![]() , and its boundary conditions are still expressed as follows according to the three support modes :
, and its boundary conditions are still expressed as follows according to the three support modes :
![]()
![]()
![]()
![]()
![]()
![]()
They contain displacement components and their first partial derivatives .
Now starting from the form of virtual work functional , consider the following variational equation
![]() (right )
(right )![]()
Integrating by parts applying the Gaussian formula gives![]()
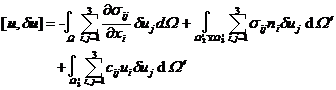
From the sum variation equation, the equilibrium equation sum of the internal force in W is obtained , and the boundary conditions on . As for the geometric constraints on , since it is not reflected in P ( u ) , it needs to be imposed , that is, when solving the variational equation , In addition to adding conditions to the variation , it must also be satisfied . Conversely , multiplying the satisfied variation by the equilibrium equation of the internal force of the elastic body W and the boundary conditions on it and making the corresponding integration , it is obvious that the Gauss formula is applied. Get the above variational equation .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In the bending problem of thin plate , the deflection w ( x , y ) of the mid-plane is taken as the undetermined function , the balance equation of the internal force of the elastic body has been satisfied by itself in the derivation process , and the boundary condition of the above plate is taken as the differential equation satisfied by w
![]()
![]()
![]()
The corresponding boundary condition is determined by the balance of internal and external forces at the edge section of the plate . Due to the complexity of the support method , the following first integrals the virtual work function of the purely elastic support to obtain the general form , and then consider other supports . The impact on each integral . Let
![]()
Substituting expressions such as B , D and internal force and integrating by parts , it can be shown that
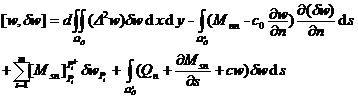
where is the inflection points arranged in sequence along the positive direction of s on the boundary .![]()
![]()
Since a load bearing can be regarded as a special case of an elastic bearing ( i.e. the case of c or ), it is only necessary to consider given deflection and rotation angle respectively on the part boundary :![]()
![]()
![]() ( The other condition can only be the elastic reaction moment )
( The other condition can only be the elastic reaction moment )
![]() ( The other condition can only be elastic reaction force )
( The other condition can only be elastic reaction force )
( ![]() can overlap ) and there is a concentrated force at the inflection point ( can be zero , especially when ) , then the corresponding external force potential energy can be written as
can overlap ) and there is a concentrated force at the inflection point ( can be zero , especially when ) , then the corresponding external force potential energy can be written as![]()
![]()
![]()
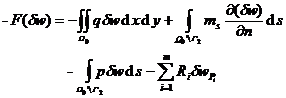
The same condition should be added to the deformation energy :
![]()
Comparing the above two equations , it can be seen that the variational problem : satisfying the imposed condition
![]()
and make
![]() ( right )
( right )![]()
The solution w of , is the solution of the definite solution problem of the following differential equation :
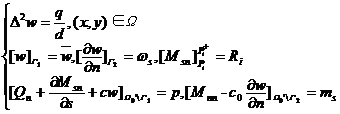
In turn , the solution w of this problem is obviously also the solution of the above variational problem , so they are equivalent .
The cylinder torsion problem takes the torsion angle w ( z ) of the cylinder cross-section as an undetermined function , and the equilibrium equation of its generalized force ( ie torque ) is a differential equation along the length of the cylinder :
![]()
Considering the case of purely elastic support first , the boundary conditions can be written as
![]()
The corresponding virtual work functional and external force potential energy are
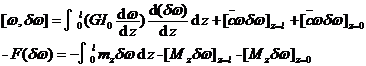
Integrate the former formula by parts , and then compare the latter formula to see that the variational equation is solved
![]() (to everything )
(to everything )![]()
The problem of is equivalent to the definite solution of the second-order ordinary differential equation above . The case where the endpoints are supported by loads can be regarded as a special case ( that is , the case of ). For the case where the endpoints are geometrically constrained , as long as the variational equation with Remove the terms related to this end and impose conditions on ω and , and the two problems are still equivalent .![]()
![]()
![]()
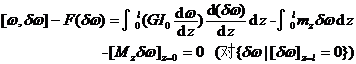
The problem of the function ω ( z ) of , is equivalent to the problem of the definite solution of the following differential equation :
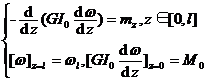
[ Thermal effect and thermal equivalent load ] In the elastic problem , the expansion and contraction of each element of the elastic body is caused by heating , thereby adjusting the distribution of stress or strain inside the elastic body. This effect is called thermal effect . The temperature distribution in the zero-strain state is set ; T is the temperature distribution after small deformation . Due to the temperature rise , the elastic body will expand ( or shrink , when ) uniformly around. In any Cartesian coordinate system , its displacement component is only related to , that is, only linear strain and no shear strains ( i 1 j ), and under the assumption of small deformation , they are linearly related to :![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where α is called the coefficient of linear expansion .
If thermal effects are considered , the total strain of the elastomer is
![]()
where is the strain without temperature difference . Under the assumption of small deformation , there are![]()
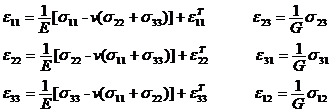 (36)
(36)
Therefore, for problems only related to shear strain, such as cylindrical torsion , the thermal effect is zero . For general spatial problems , it can be set that
![]()
then there are
![]() or
or![]()
![]() It can be regarded as the zeroth order term of the total strain . It shows that in the unstressed state ( such as the elastic body is completely free to expand ) , the elastic body also has thermal strain ; and in the unstrained state ( such as its boundaries are all constrained ) , the elastic body is due to The temperature rise can produce thermal stress - D . Now let = D , then there is
It can be regarded as the zeroth order term of the total strain . It shows that in the unstressed state ( such as the elastic body is completely free to expand ) , the elastic body also has thermal strain ; and in the unstrained state ( such as its boundaries are all constrained ) , the elastic body is due to The temperature rise can produce thermal stress - D . Now let = D , then there is![]()
![]()
![]()
![]()
![]()
![]()
in the formula
![]()
For the plane strain problem , since ( note that it is not ), the third formula of (36) can be directly used :![]()
![]()
![]()
Substituting into the first two equations of (36) , the zero-order term is obtained . It can be obtained from the corresponding matrix D![]()
![]()
![]()
For the plane stress problem , it is assumed that the value of the zero-order term of the first quadratic formula (36) does not change , so according to the corresponding matrix D , we can get![]()
![]()
For the thin plate bending problem , the temperature rise distribution function can be written approximately as
![]()
where and can be regarded as the average and gradient along the thickness, respectively . Then the total strain![]()
![]()
![]()
![]()
The stress and bending moment corresponding to the zero-order term are![]()
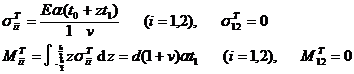
This indicates that the bending moment of the plate is only proportional to the gradient of the temperature rise , and is not affected by the temperature rise distribution on the midplane of the plate .![]()
![]()
For space problems , the first term related to and in the virtual work functional should be rewritten as![]()
![]()
![]()
![]()
The second integral on the right side of the equation is the term due to the thermal effect . There is no u in it . This shows that in the deformation energy , the thermal effect part is linear to u , and it may be classified into the external force potential energy . This is the same as the elastic reaction force Part of the generated external force potential energy ( C u , u ), because it is quadratic with respect to u , is classified as a virtual work functional on the contrary . To highlight , integrate this term by parts :![]()
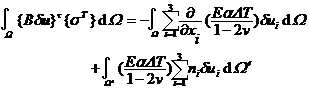
Comparing the integrand in the comparison , it can be seen that the thermal effect is like adding physical force and surface force to the elastic body :![]()
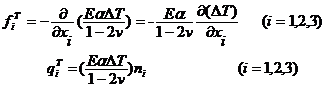
These forces can be called thermal equivalent loads . It is the gradient of the fully constrained thermal (normal) stress . When constant , the thermal equivalent load is only the surface force.![]()
![]()
![]()
![]()
For the thin plate bending problem, due to the thermal effect virtual work function has one more integral, it can also be classified into the external force potential energy and two parts integration can be obtained.
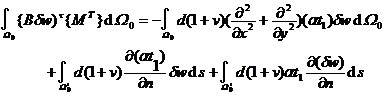
Comparing the integrand in the comparison, it can be seen that the thermal effect is the same as the result of applying a surface force to the upper plate surface of the thin plate and applying a transverse linear force and a moment around the tangential direction to the side surface of the single-width boundary . When taken as a constant, the thermal equivalent load is only a moment .![]()
![]()
![]()
![]()
![]()
![]()
[ Displacement method and force method ] The displacement method takes the displacement , generalized displacement or the warping function y as in the torsion problem of the cylinder as undetermined; the force method takes the stress or the following stress function F as the undetermined. Just take the cylinder torsion problem as an example to illustrate.
For a simply connected region W , the equilibrium equation guarantees the existence of a function F ( x , y ) such that ![]()
![]()
This F ( x , y ) is called the torsional stress function. Compare it with the above physical equation to get the relationship between it and the warping function:
![]()
Since the necessary and sufficient conditions for the existence of displacement w or y are : ![]()
Coordination equation:
![]()
Since there is no external force on the side, that is , we can get![]()
![]()
This means that F takes a constant along the section boundary (maybe zero), so that
Boundary conditions:
![]()
Let then be a boundary value problem of the first kind of Poisson equation:![]()
![]()
solution. According to the condition that the moment of the end face z = l is M :
![]()
torsion rate
![]()
![]() It can also be regarded as "stress" and boiled down to the following variational problem: to satisfy , and to make the total potential energy
It can also be regarded as "stress" and boiled down to the following variational problem: to satisfy , and to make the total potential energy![]()
![]()
Take the extremum solution.
Note that the force method is reduced to the solution of the first type of boundary value problem of the Poisson equation, which is simpler than the displacement method reduced to the second type of boundary value problem. But when the region is complex connected, the coordination condition or the singularity of the displacement must also satisfy the integral condition at each inner boundary.![]()
![]()
where is the enclosed area, and p is the connectivity of the region W. In this case, the constant value is also undetermined, so when the section is a region with connectivity p , the force law boils down to the Poisson equation with p integration conditions and the first boundary value containing p undetermined constants The problem is more complicated than the displacement method.![]()
![]()
![]()
![]()
![]()
In addition to these two methods, there is also a hybrid method that uses both displacement and stress as undetermined functions. If applied properly, the solution method of the problem can be greatly simplified.