§ 3 Practical geometric construction
1. Drawing of
regular polygons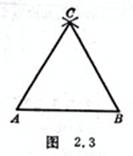
[ Construct an equilateral triangle with known side lengths ] It is known that AB is equal to the side length . Take A and B as the center of the circle and AB as the radius to draw an arc to intersect with C , and connect AC and BC , which is the equilateral triangle (Figure 2.3 ) .![]()
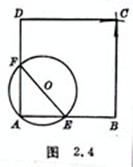
[ Make a square with the known side length ] It is known that AB is equal to the side length . Take any point O outside AB as the center of the circle , and OA as the radius to draw a circle to meet AB at E. Connect EO and extend the intersecting circle at F , connect AF and extend and intercept AD= AB . Take B and D as the center respectively, and AB as the radius to draw an arc to intersect C , connect BC , DC , and □ ABCD is the desired square ( Figure 2.4 ).
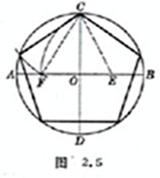
[ The circumscribed circle is known as a regular pentagon ] Through the center O , draw the diameters AB and CD that are perpendicular to each other , bisect OB at E , take E as the center, EC as the radius, and draw an arc intersecting OA at F , with CF as the radius on the circumference Sequentially truncate and connect the points, that is, the required regular pentagon ( Figure 2.5 ). You can also refer to the regular decagon method ( see the dotted line in Figure 2.11 ).
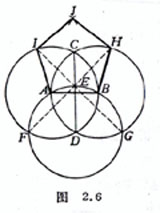
[ Construct a regular pentagon with known side lengths ] It is known that AB is equal to the side length . With A and B as the center and AB as the radius, draw two circles that intersect at C and D and connect CD . With D as the center and AB as the radius, draw a circle , intersect CD at E , intersect A circle at F , intersect B circle at G , connect FE , GE , and extend to meet B , A circle at H , I. Take H , I as the center and AB as the radius to draw an arc to intersect atJ , connecting JI , IA , BH , HJ , together with AB is the required regular pentagon ( Figure 2.6 ).
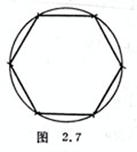
[ The circumscribed circle is known to be a regular hexagon ] Use the radius of the circumscribed circle to cut sections in sequence on its circumference , and connect the points, that is, the regular hexagon sought ( Figure 2.7 ).
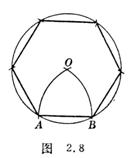
[ Construct a regular hexagon with known side length ] Knowing that AB is equal to the side length , take A , B as the center, AB as the radius, and draw an arc to intersect O , take O as the center, and AB as the radius to draw a circle . Make the desired regular hexagon ( Figure 2.8 ).
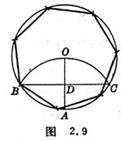
[ The known circumscribed circle is a regular heptagon ( approximate method )] Taking any point A on the circumference as the center of the circle, with the radius of the same circle as the radius, draw an arc to intersect the circumference at B , C , connect BC , AO , and intersect at D. Take BD as the radius ( It should be slightly larger than BD when drawing ) Cut sections in sequence on the circumference, and connect the points, that is, the required regular heptagon ( Figure 2.9 ).
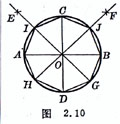
[ The known circumscribed circle is a regular octagon ] Make the diameters AB and CD which are perpendicular to each other through the center O. Take A , B , D as the centers respectively, and draw arcs with any length as the radius to intersect at E , F , connecting EO , FO , and Extend the intersection circle at G , H , I , J , and connect the eight points in sequence, which is the required regular octagon ( Figure 2.10 ).
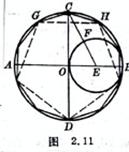
[ The circumscribed circle is known to be a regular decagon ] Through the center O , make the diameters AB and CD that are perpendicular to each other , draw a circle E with OB as the diameter , connect EC and intersect the circle E at F. Take CF as the radius and make successive sections on the circumference , and connect the points, that is, the desired regular decagon ( Figure 2.11 ).
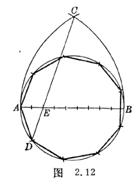
[ The known circumscribed circle is an arbitrary regular polygon ( approximate method )] Divide the diameter AB n into equal parts ( n is the number of sides ), take A , B as the center, AB as the radius, draw an arc to intersect C , connect C with the second division Point E , and extend the intersection circle to D , take AD as the radius to cut the circle in sequence, and connect the points, that is, the regular n -gon ( regular nonagon in Figure 2.12 ).
2.
Ellipse drawing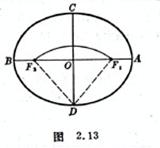
The long and short axes ( 2 a, 2 b ) are known to make an ellipse, and the method is as follows:
[ Track method ] Take the long axis AB = 2 a and the short axis CD = 2 b , perpendicularly bisect each other at O , take D as the center, a as the radius, and draw an arc to intersect AB at . The two ends of the line of 2 a are fixed on the nails, and then the line is tightened with a pencil, and the curve drawn by moving the pencil is an ellipse ( Figure 2.13 ).![]()
![]()
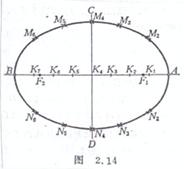
[ Focus method ] The same as the trajectory method , first draw a point , divide AB 8 equally, each point in the middle is the center of the circle, draw an arc for the radius, draw the arc for the center of the circle, draw an arc for the radius, and the two intersect at the sum . Then connect these intersection points together with A and B with smooth curves in turn, that is, approximate the desired ellipse ( Figure 2.14 ).![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
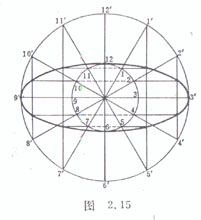 [ Compression method ] Draw two concentric circles with the major and minor axes as the diameter, and divide the circumference into 12 equal parts ( the bisector of the small circle is 1-12 , and the bisector of the large circle corresponds to ) . Connect and 1-11 , 2-10,4- 8 , 5 - 7 , and extended, will intersect with 1 - 11 , 5 - 7; with 2 - 10 , 4 - 8; with 1 - 11 , 5 - 7; with 2 - 10 , 4 - 8 ( total 8 indivual
[ Compression method ] Draw two concentric circles with the major and minor axes as the diameter, and divide the circumference into 12 equal parts ( the bisector of the small circle is 1-12 , and the bisector of the large circle corresponds to ) . Connect and 1-11 , 2-10,4- 8 , 5 - 7 , and extended, will intersect with 1 - 11 , 5 - 7; with 2 - 10 , 4 - 8; with 1 - 11 , 5 - 7; with 2 - 10 , 4 - 8 ( total 8 indivual![]()
![]()
![]()
![]()
![]()
![]() ) , together with the four vertices, are sequentially connected by smooth curves, which approximate the desired ellipse ( Fig. 2.15 ).
) , together with the four vertices, are sequentially connected by smooth curves, which approximate the desired ellipse ( Fig. 2.15 ).
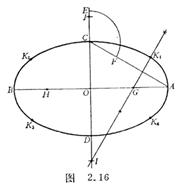 [ Circular arc method ] Take the long axis AB = 2 a , the short axis CD = 2 b , bisect each other at O , take OE = OA , take C as the center and CE as the radius, draw an arc to intersect AC at F , and make AF The vertical bisector intersects AB at G , and intersects the extended line of CD at I. Make OH = OG , OJ =OI . Take I , J as the center and IC as the radius to draw an arc, and G , H as the center, GA as the radius If the arc is drawn, then the four arcs are connected to approximate the desired ellipse( Figure 2.16 ).
[ Circular arc method ] Take the long axis AB = 2 a , the short axis CD = 2 b , bisect each other at O , take OE = OA , take C as the center and CE as the radius, draw an arc to intersect AC at F , and make AF The vertical bisector intersects AB at G , and intersects the extended line of CD at I. Make OH = OG , OJ =OI . Take I , J as the center and IC as the radius to draw an arc, and G , H as the center, GA as the radius If the arc is drawn, then the four arcs are connected to approximate the desired ellipse( Figure 2.16 ).
3.
Arc lofting method
 In civil engineering, due to the limitation of various construction conditions, it is not possible to draw an arc with one turn of the compass. The following method can be used to directly enlarge the sample at the construction site . This method can release any large radius in a limited plane. The real sample of the arc is convenient for workers to grasp .
In civil engineering, due to the limitation of various construction conditions, it is not possible to draw an arc with one turn of the compass. The following method can be used to directly enlarge the sample at the construction site . This method can release any large radius in a limited plane. The real sample of the arc is convenient for workers to grasp .
[ Arc with known chord length and vault height ]
method![]()
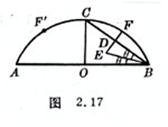
Make AB equal to the chord length, make CO to bisect AB vertically , and make CO equal to the height of the arch, connect BC , and make the mid-perpendicular line DE of BC . The bisector made to intersect DE at E , and take DF=DE on the extension line of ED , then F is the dividing point . From the symmetry, the symmetrical point of F is also the dividing point . Repeat the above steps to obtain each dividing point, and connect each dividing point with a smooth curve in sequence, which is the desired arc ( Figure 2.17 ). ). This method has a clear concept, fewer steps, and the smallest footprint .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
method![]()
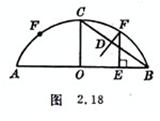 Make AB equal to the chord length, make CO to bisect AB vertically , and make CO equal to the arch height . Make the mid-perpendicular DF of BC , and cut OE=CD . Through E , make the vertical line of AB intersect DF at F , then F is the bisector of . From the symmetry, the symmetric point of F is also a sub-point . Repeat the above steps to obtain each sub-point, and connect each sub-point with a smooth curve in sequence, which is the desired arc ( Figure 2.18 ). This method steps least .
Make AB equal to the chord length, make CO to bisect AB vertically , and make CO equal to the arch height . Make the mid-perpendicular DF of BC , and cut OE=CD . Through E , make the vertical line of AB intersect DF at F , then F is the bisector of . From the symmetry, the symmetric point of F is also a sub-point . Repeat the above steps to obtain each sub-point, and connect each sub-point with a smooth curve in sequence, which is the desired arc ( Figure 2.18 ). This method steps least .![]()
![]()
![]()
![]()
![]()
![]()
![]()
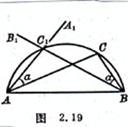 [ The chord length and any point on the arc are known to make an arc ]
The known AB is the chord length , and C is a point on the known arc . Take BC as the side to make an angle . Then take AC as the side to make an angle in the same direction . point . When a is taken as a series of values, a series of points on the arc are obtained, and the points are connected in sequence with a smooth curve, that is, the arc sought ( Figure 2.19 ). This method is most suitable for using theodolite and compass The instrument is used to measure the arc of a large radius .
[ The chord length and any point on the arc are known to make an arc ]
The known AB is the chord length , and C is a point on the known arc . Take BC as the side to make an angle . Then take AC as the side to make an angle in the same direction . point . When a is taken as a series of values, a series of points on the arc are obtained, and the points are connected in sequence with a smooth curve, that is, the arc sought ( Figure 2.19 ). This method is most suitable for using theodolite and compass The instrument is used to measure the arc of a large radius .![]()
![]()
![]()
![]()
Fourth, the
problem of geometric drawing
The so-called elementary geometric drawing problem refers to the use of rulers and compasses without scales to make drawings . If geometric figures can be made by using rulers and compasses a finite number of times, it is called the possibility of drawing, or the Euclidean method of drawing is possible , otherwise it is called mapping impossible .
Many plane figures can be made with rulers and compasses, such as the regular pentagons, regular hexagons, regular octagons, regular decagons, etc. listed above . Others cannot be made, such as regular heptagons, regular nonagons , regular 11-gon, etc. These polygons can only be approximated by the approximate drawing method . How to judge which mapping is possible and which is impossible? Until more than a hundred years ago, this problem was completely solved by algebraic methods, that is, a criterion for the possibility of ruler and compass mapping was given: the necessary and sufficient condition for the possibility of mapping is that the unknown unknown must be required in this mapping problem. Quantities can be calculated from a number of known quantities through a finite number of rational operations and square root operations . For thousands of years, many mathematicians have spent a lot of energy trying to solve the so-called " three major problems of geometry " :
![]() The cube product problem is to make a cube whose volume is twice the volume of a known cube .
The cube product problem is to make a cube whose volume is twice the volume of a known cube .
![]() The problem of trisecting an angle, that is, trisecting a given angle .
The problem of trisecting an angle, that is, trisecting a given angle .
![]() The problem of making a circle square is to make a square so that its area is equal to the area of a known circle .
The problem of making a circle square is to make a square so that its area is equal to the area of a known circle .
Later, it has been strictly proved that these three problems cannot be drawn with rulers and gauges .