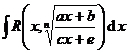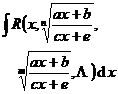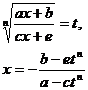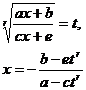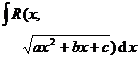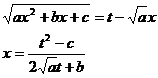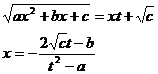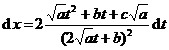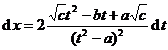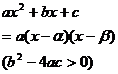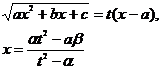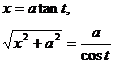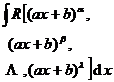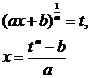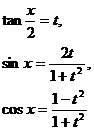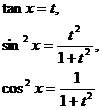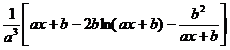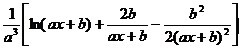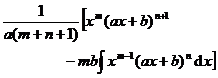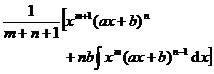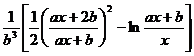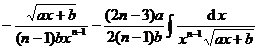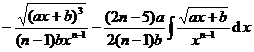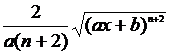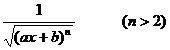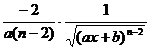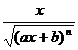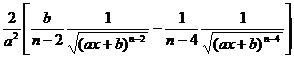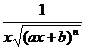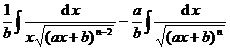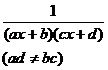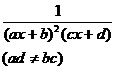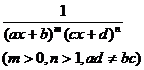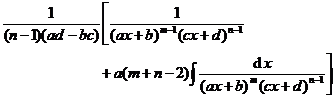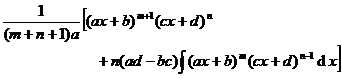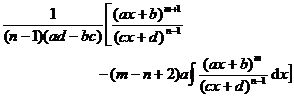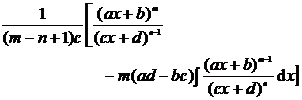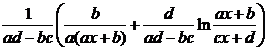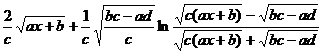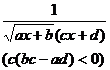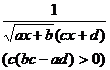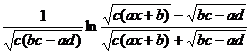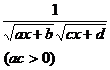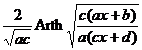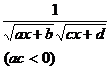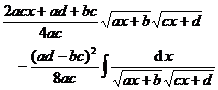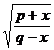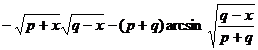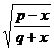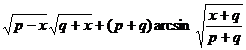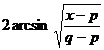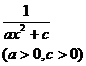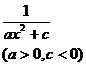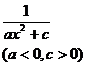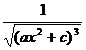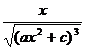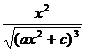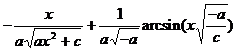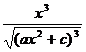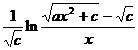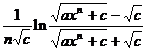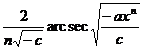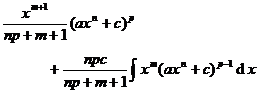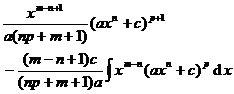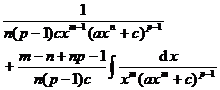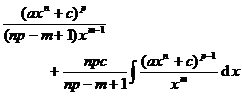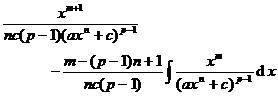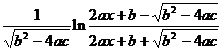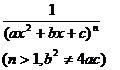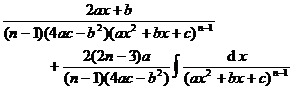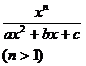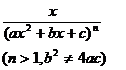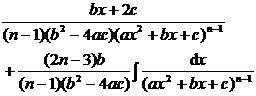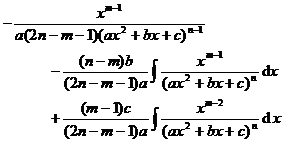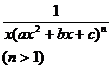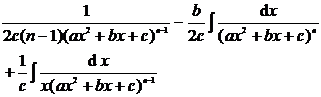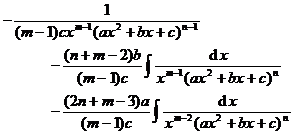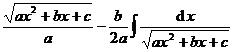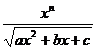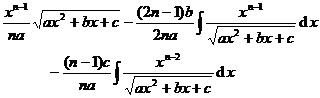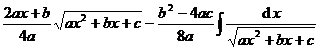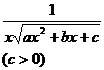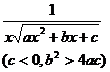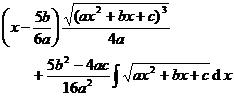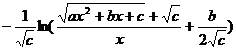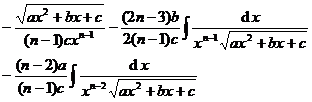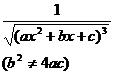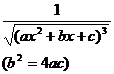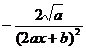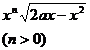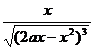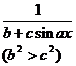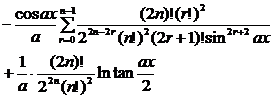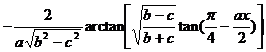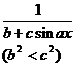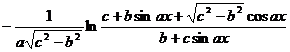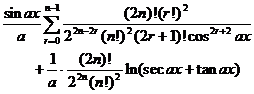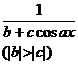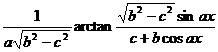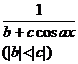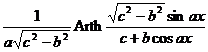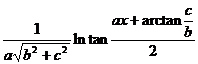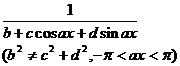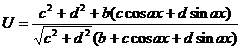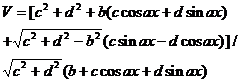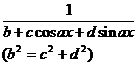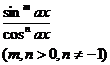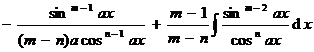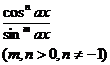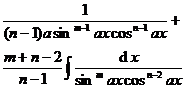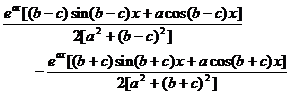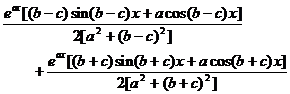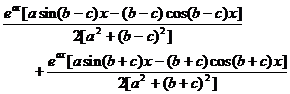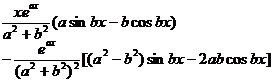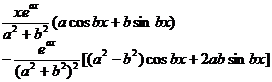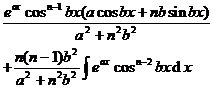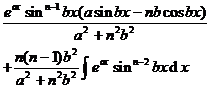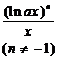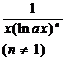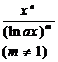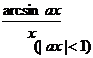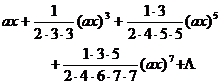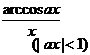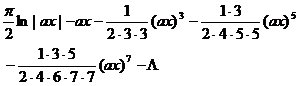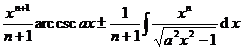Chapter 6 Integral Science

Chapter 6 Integral Science

This chapter summarizes the basic concepts, properties and calculation methods of ordinary integrals, generalized integrals and integrals with parameters of univariate functions. The integral inequality and some approximate calculation formulas of integral are briefly listed, and various applications of integral in practice are briefly listed; indefinite integral table and definite integral table are compiled .

§1 Integration of functions of one variable

First, the basic concept of integral

[indefinite integral (original function)] if over the given interval [ a , b ]

Then F ( x ) is called a primitive function of f ( x ) on the interval [ a , b ] .

If f ( x ) has an original function F ( x ) , then it must have infinitely many original functions of the form

(where C is an arbitrary constant) family of functions, so use the notation

Represents the totality of primitive functions of f ( x ), called the indefinite integral of f ( x ) .

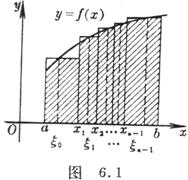
[Definite integral·Riemann integral] Set the function f ( x ) on the interval [ a , b ] . Divide the interval [ a , b ] into several parts by any method , and let λ be ( i = 0, 1, 2, ... , n - 1) . Take any point ( i = 0, 1, 2, ... , n - 1) in each small interval [ ], and make a sum ( Figure 6.1 ) . When λ → 0 , if the limit

exists, then this limit is called the definite integral of the function f ( x ) over the interval [ a , b ] , denoted as

At this time, the function f ( x ) is called an integrable function (Riemann integrable) on the interval [ a , b ] , a and b are called the lower and upper limits of the integral, respectively, f ( x ) is called the integrand function, x is the integral variable, " " is the integral sign .

[Newton-Leibniz formula] If the function f ( x ) is continuous on the interval [ a , b ] , or piecewise continuous, then f ( x ) has the original function on [ a , b ] , let F ( x ) ) is a primitive function of f ( x ) on [ a , b ] , then

This is called the Newton-Leibniz formula, or the Fundamental Theorem of Calculus, and it states the intrinsic connection between definite and indefinite integrals .

[integrable functions and their properties]

1° If the function f ( x ) is continuous on the interval [ a , b ] , then f ( x ) is integrable .

2° If the function f ( x ) is bounded on [ a , b ] and has only finitely many discontinuities, then f ( x ) is integrable .

A 3° monotone bounded function must be integrable .

A 4° integrable function must be bounded .

5° If the function f ( x ) is integrable, then | f ( x )| and kf ( x ) ( k is a constant) are also integrable .

6° If the functions f ( x ) and g ( x ) are integrable, their sum, difference and product are also integrable .

7° If the function f ( x ) is integrable over [ a , b ] , then f ( x ) is also integrable over any partial interval [ α , β ] in [ a , b ] . On the contrary, if [ a , β ] is integrable , b ] is divided into several partial intervals, and f ( x ) is integrable over each partial interval , then it is integrable over the entire interval [ a , b ] .

[Integral median theorem] silly silly silly

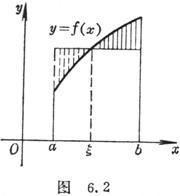
1° If the function f ( x ) is continuous on the interval [ a , b ] (Fig. 6.2 ), then there is at least one number ξ ( a < ξ < b ) in the interval [ a , b ] such that

2° If the functions f ( x ) and g ( x ) are bounded and integrable on the interval [ a , b ] , f ( x ) is continuous, and g ( x ) is invariant in the interval [ a , b ] , then There is at least one number ξ ( a < ξ < b ) in the interval [ a , b ] such that

This is called the first median theorem on integrals .

3° If the functions f ( x ) and g ( x ) are bounded and integrable on the interval [ a , b ] , and f ( x ) is monotonic on [ a , b ] , then on the interval [ a , b ] ] at least one number ξ ( a < ξ < b ) exists such that

This is called the second median theorem for integrals .

4° In addition to this condition, if f ( x ) is non-negative and monotonically decreasing (generalized), then

( a < ξ < b )

If f ( x ) is non-negative and monotonically rising (generalized), then

( a < ξ < b )

Second, the integral inequality

Suppose f ( x ), g ( x ) are integrable over the interval [ a , b ] , then there are the following inequalities:

1° If f ( x ) ≤ g ( x ) on the interval [ a , b ] , then

≤

2° , then

m ≤ ≤ M

3° ≤

4° Schwartz's inequality

≤

5° Herder's inequality set k > 1 , > 1, , then

≤

The equal sign is only true when the sign of f ( x ) g ( x ) is fixed and ( c is a constant), and when k = k ' = 2, it is Schwartz's inequality .

6° Minkowski's inequality set r > 0 , then

≤ ( r ≥ 1)

≥

( r < 1, f ( x ) and g ( x ) have the same sign on [ a , b ] )

The equal sign only holds when f ( x ) = cg ( x ) ( c is a constant ) .

The 7° Bessel inequality is assumed ( n is a positive integer) to be a normal orthogonal system on [ a , b ] :

but

≤

8° Hardy's Inequality Let f ( x ) be differentiable and rising on [ 0 , ∞ ), f '( x ) is continuous, f (0)=0 , p > 1, then

The equal sign only holds when f ( x ) ≡ 0 .

3. How to find the original function

1. Indefinite Integral Rule

( a , b are constants ) ( linear operation )

( variable substitution )

( Partial credits )

( Allotment points )

2. Integral of rational fractions

[Forming into fundamental true fractions] Let R ( x ) be a true fraction with real coefficients, then the integral of R ( x ) can be transformed into the integral of the fundamental true fractions (Chapter 1, § 1) it decomposes ,and

The formula is still a rational function, and is still a true fraction, H ( x ) is generally a transcendental function (logarithmic function and arctangent function) .

[Ostello Glatsky's method] The integral of any true fraction can be written as

where , is a true fraction,

The coefficients of the sum can be obtained from the relational expression using the undetermined coefficient method.

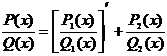
found in .

3 . Table of Variable Substitution Formulas for Rational Function Integrals

R is the rational function in the table

Point type	Variable substitution formula
( n is an integer) ( m , n are integers)	where r is the least common multiple of n , m , ...
when a > 0 when c > 0

	(or x = a sh t , ) ( or x = a cos t , ) ( or x = a ch t , )	(or d x = a ch t d t ) (or d x =- a sin t d t ) (or d x =- a sh t d t )
Point type	Variable substitution formula
(where is the fraction)	Let m be the least common multiple of the denominator ,

4 . Indefinite integral table

The integral constants are omitted from the table, and ln g ( x ) refers to ln | g ( x ) |.

[ Basic Points Table ]


( constant )

	ln x

( a > 0)



	or
	or




th x
cth x
sech x
csch x
	th x
	-cth x
( a > 0)
(\| x \|<\| a \|)	or
(\| x \|>\| a \|)	or


	or
	or
	or
	or
	or
	or or or

[ Integration of rational expressions including ax + b ] ( )










( )


( )	or or

[ Included points ] ( )


	or




	or
( )
( )

[ Included points ]







	or

[ integral of rational expressions containing ]

[ Included points ]


( a > 0 )
( a < 0 )
( a > 0 )
( a < 0 )

( a > 0 )
( a < 0 )
( n > 0 )


( n > 0 )
( c > 0 )
( c < 0 )
( n > 1)
( a > 0 )
( a < 0 )




( n > 0 )

( a > 0 )
( a < 0 )

( c > 0 )
( a >0 , c < 0 )

( n > 1 )

[ Included points ]


( n > 0)
( n >0, c >0)
( n >0, c <0)
( )


( n >0 , p >1 )

( n >0 , p >1 )

[ integration of rational expressions including ) ]









f ( x )

[ Included points ]

f ( x )




f ( x )

( n > 1 )

[ Included points ]






( n is a positive integer )
( n is a positive integer )
( n is a positive integer )
	or

( n is an integer ) ( n is a positive integer ) ( n is a positive integer )



	( when When , take the positive sign; otherwise, take the negative sign . k is an integer )
	( when When , take the positive sign; otherwise, take the negative sign . k is an integer )

[ Included points ]






( n is a positive integer )
( n is a positive integer )
( n is a positive integer ) ( n is an integer ) ( n is a positive integer ) ( n is a positive integer )	or

	( when When , take the positive sign; otherwise, take the negative sign . k is an integer )
	( when When , take the negative sign; otherwise take the positive sign . k is an integer )