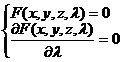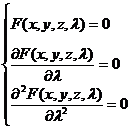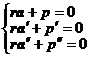§ 11 Developable surfaces
[ Envelope Surfaces for Single Parameter Surface Family ]
|
Definition |
equation |
|
A surface whose envelope is tangent to all surfaces of the surface family S λ is called the envelope of S λ .
The limit position of the intersection of two adjacent surfaces in the ridge family S λ is called the characteristic line of S λ , and the envelope of the characteristic line (if any) is called the ridge line of the family S λ |
|
[ Envelope Surface for Single Parameter Plane Family ]
|
Definition and Properties |
Equations and Graphics |
|
|
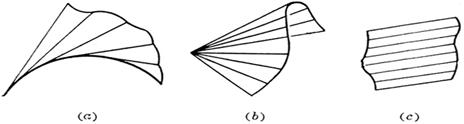
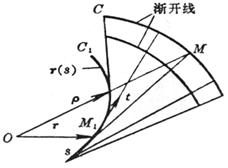
The envelope surface of the single-parameter plane family of developable surfaces is called the family's developable surface . The envelope surface is the surface, cone or cylinder formed by the tangent of the space curve (Fig. ( a ), ( b ), ( c ) ) |
The one-parameter plane family equations are ra (λ)+p(λ)=0(λis a parameter) Its envelope satisfies the system of equations where is the normal vector of the plane family |
|
|
|
||
|
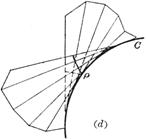
The limit position of the intersection of two adjacent planes in the ridge plane family is called the feature line of the family, and the envelope of the feature line (if it exists) is called the ridge line of the family, which divides the envelope surface into two leaves, with the ridge Lines as "sharp bobbins" of surfaces (figure ( d ) ) |
The ridge line satisfies the system of equations |
|
|
|
||
Example The envelope surface of the normal surface of a space curve C is called the polar developable surface of C , which is the locus of the curvature axis (that is, passing through the center of curvature and parallel to the binormal) . The equation of the ridge line is
![]()
where is the curvature radius of curve C , is the torsion radius of curve C ,![]()
![]()
![]()
![]()
[ Involutes and Involutes of Space Curves ]
|
Definition and Properties |
Equations and Graphics |
|
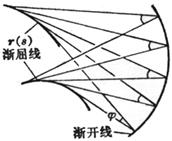
The involute curve that is orthogonal to the curve r ( s ) on a developable surface of the space curve r ( s ) is called the involute of r ( s ) . The distance between the two involutes along the tangent of r ( s ) remains constant (right image) |
|
|
An involute space curve r ( s ) is an involute for its involute, that is, a family of normal envelopes of the involute . A point M 1 of the involute C 1 falls on the axis of curvature of the corresponding point M of C. (The lower figure on the upper page) If this family of normals forms a developable surface, rotate a fixed angle on the normal surface, and the resulting normals still form a developable surface (right) |
where is the radius of curvature, and is the intersection angle between the tangent of the involute and the principal normal |