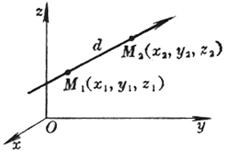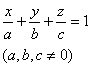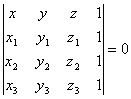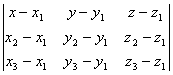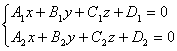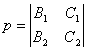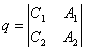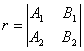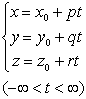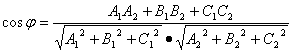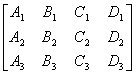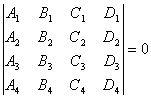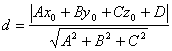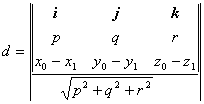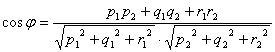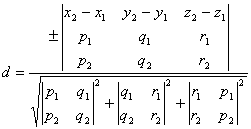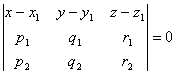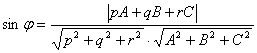§4 Lines and planes in space
The direction of the straight line
|
name and description |
graphics |
|
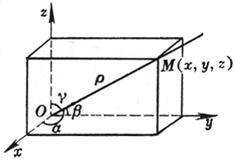
[ direction angle ] The angle a , b , g of the straight line OM passing through the origin O and the three coordinate axes is called the direction angle of the line ( the direction of OM is the direction away from the origin O ) : [ direction cosine ] The cosine of the direction angle of a line is called the direction cosine: In the formula , l 2 + m 2 + n 2
= 1 |
|
|
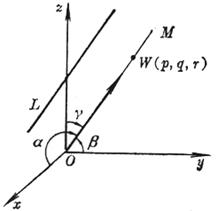
[ Number of directions ] The coordinates ( p , q , r ) of any point W on the straight line OM passing through the origin and parallel to the straight line L are called the number of directions of the straight line L, and
|
|
|
name and description |
graphics |
|
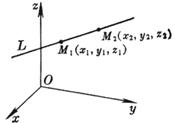
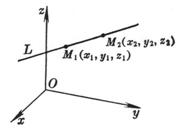
[ Direction cosine of a line passing through two points ]
in the formula At this time, the positive direction of the straight line is the direction from M 1 ( x 1 , y 1 , z 1 ) to M 2 ( x 2 , y 2 , z 2 ) .
|
|
The equation of the plane
|
Equations and Graphics |
Description |
|||||
|
[ intercept ] |
|
a, b, c are called the intercepts of the plane on the three coordinate axes, respectively
|
||||
|
[ dot French ]
( A , B , C are not equal to zero at the same time )
|
|
The plane passes through the point M ( x 0 , y 0 , z 0 ) and the number of directions of the normal N is A , B , C
|
||||
|
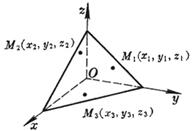
[ Three-point type ] |
|
The plane passes through three points : M 1 ( x 1 , y 1 , z 1 ) M 2 ( x 2 , y 2 , z 2 ) M 3 ( x 3 , y 3 , z 3 )
|
||||
|
or
|
||||||
|
equation |
with graphics |
Description |
||||
|
[ General formula ] Ax + By + Cz + D = 0 ( A , B , C are the direction numbers of the normal of the plane, and are not equal to zero at the same time ) |
|
When D = 0 , the plane passes through the origin When A = 0 ( or B = 0 , or C = 0) , the plane is parallel to the x - axis ( or y - axis, or z - axis ) When A = B =0 ( or A = C =0 , or B = C =0) , the plane is parallel to the Oxy plane ( or Ozx , or Oyz ) |
||||
|
[ normal type ]
( a , b , g are the direction angles of the normal line of the plane, p 3 0 is the length of the normal line, that is, the distance from the origin to the plane )
|
|
The general formula of the plane can be transformed into the normal formula , which is called the normalization factor of the plane. When D < 0 , the positive sign is taken; when D > 0 , the negative sign is taken.
|
||||
|
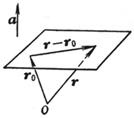
[ vector ] ( r - r 0 ) × a = 0
|
|
The plane passes through the end point of the vector radius r 0 and is perpendicular to the known vector a , r is the vector radius of any point on the plane
|
||||
The equation of a straight line
|
Equations and Graphics |
Description |
||
|
[ General formula ( or face-to-face )] L
|
Taking the straight line L as the intersection of two planes, its number of directions is
|
||
|
[ Symmetrical ( or parametric )]
or |
The straight line L passes through the point M ( x 0 , y 0 , z 0 ) and has the number of directions p , q , r
|
||
|
Equations and Graphics |
Description |
||
|
[ two-point type ]
|
The straight line L passes through two points M 1 ( x 1 , y 1 , z 1 ) and M 2 ( x 2 , y 2 , z 2 )
|
||
|
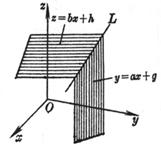
[ projective ] L |
|
The straight line L is the intersection of the two planes y = ax + g and z = bx + h ; it passes through the point (0, g , h ) and has direction numbers 1, a , b
|
|
|
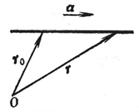
[ vector ] r = r 0 + t a (- ¥ < t < ¥ )
|
|
The straight line L passes through the end point of the vector radius r 0 and is parallel to the known vector a , where r is the vector radius of any point on L
|
|
4. Interrelationship between points, lines and planes in space
|
Equations and Graphics |
Formula and Explanation |
|
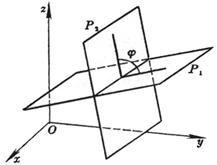
[ Included angle between two planes ] P 1 A 1 x + B 1 y + C 1 z + D 1 = 0 P 2 A 2 x + B 2 y + C 2 z + D 2 = 0
|
where is the dihedral angle of the two planes P 1 and P 2
|
|
Equations and Graphics |
Formula and Explanation |
|
[ Condition of plane bundle × collinearity of three planes ] P l ( A 1 x + B 1 y + C 1 z + D 1 ) + l ( A 2 x + B 2 y + C 2 z + D 2 ) = 0 ( l is a parameter, - ¥ < l < ¥ )
[ Condition of plane handle × four planes co-point ] P l m ( A 1 x + B 1 y + C 1 z + D 1 ) + l ( A 2 x + B 2 y + C 2 z + D 2 ) + m ( A 3 x + B 3 y + C 3 z + D 3 ) = 0 ( l , m are two independent parameters, - ¥ < l , m < ¥ ) |
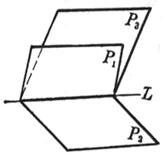
For a definite value of l, P l represents an intersection of two planes P 1 and P 2 The plane of the line L , when l takes all values, the whole of the plane represented by P l passing through L is called the plane beam, and L is called the axis of the beam . Let P 3 be A 3 x + B 3 y + C 3 z + D 3 = 0 , then the condition for the collinearity of the three planes P 1 , P 2 , P 3 is a matrix
The rank of is equal to 2.
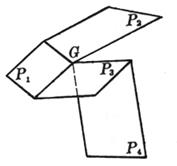
For a pair of definite values of l , m , P l m represents a plane passing through the intersection G of the three planes P 1 , P 2 and P 3 , when l , m take all values, P l m represents the plane passing through G The whole of is called the plane handle, and G is called the vertex of the handle . Assuming that P 4 is A 4 x + B 4 y + C 4 z + D 4 = 0 , the condition for the common points of the four planes P 1 , P 2 , P 3 , and P 4 is the determinant
|
|
[ distance between points and faces ] normal x cos a + y cos b + z cos g - p = 0 General formula Ax + By + Cz + D = 0
|
d method = | x 0 cos a + y 0 cos b + z 0 cos g - p | where d is the distance from point M ( x 0 , y 0 , z 0 ) to the plane
|
|
Equations and Graphics |
Formula and Explanation |
|
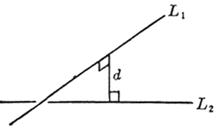
[ distance of dotted line ] L
|
where d is the distance from the point M ( x 0 , y 0 , z 0 ) to the straight line L , i , j , k are the unit vectors on the three coordinate axes, and the outermost symbol “ | | ” represents the modulus of the vector
|
|
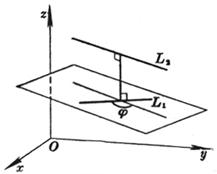
[ Included angle between two straight lines ] L 1 L 2
|
where j is the angle between the two straight lines L 1 and L 2
|
|
[ The shortest distance between two non-parallel lines ] L 1 L 2
|
The so - called shortest distance refers to the distance between the common vertical line of L 1 , L 2 and the intersection of the two lines . The equation of the plane is
|
|
|
|
|
Equations and Graphics |
Formula and Explanation |
|
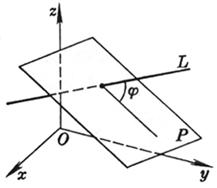
[ The angle between the line and the plane ] L P Ax + By + Cz + D = 0
|
where j is the angle between the straight line L and the plane P
|
[ Parallel and perpendicular conditions of straight lines and planes ]
|
parallel condition |
vertical condition |
|
line to line face to face line and surface
|
p 1 p 2 + q 1 q 2 + r 1 r 2 = 0
A 1 A 2 + B 1 B 2 + C 1 C 2 = 0
|