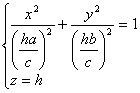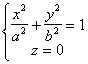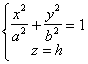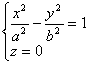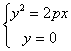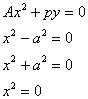§ 6 Quadric surface _
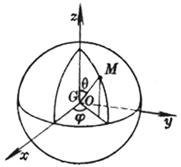
1. Spherical
[ Equation, center and radius of a sphere ]
|
Equations and Graphics |
Center and Radius |
||
|
or
( Spherical coordinate equation . In the formula, j is the longitude , and q is the co-latitude )
|
|
Center G (0,0,0 ) Radius R |
|
|
or ( j and q in the spherical coordinate equation are the same as above )
|
|
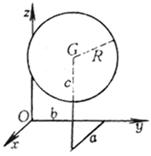
Center G ( a,b,c ) Radius R
|
|
|
Equations and Graphics |
Center and Radius |
||
|
|
ball center radius |
||
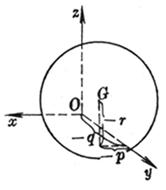
[ The tangent and normal of the sphere ] Suppose a plane P passes through a point M on the sphere and is perpendicular to the radius GM , then P is called the tangent of the sphere at M. The straight line MG is called the normal of the sphere at the point M.
Let the spherical equation be
![]()
Then the tangent equation of the sphere at the point M ( ![]() ) is
) is
![]()
The normal equation of the sphere at the point M ( ![]() ) is
) is
![]()
[ Intersection angle of two spheres ] Set two spheres
![]() =0
=0
![]() =0
=0
The intersection angle of two spheres refers to the angle between the two tangent planes at the intersection point , denoted by q , then
![]()
Since the coordinates of the intersection point are not included in the formula, the intersection angles of the points on the intersection of the two spheres must be equal .
The orthogonal condition of the two spheres is
![]()
[ Spherical bundle · Root surface of two spheres ] set
![]()
In the formula and as defined in formula (1) , and are parameters , there are![]()
![]()
![]()
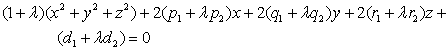
A certain value of the pair represents a sphere . When all values are taken , the whole of the spheres represented is called a spherical bundle . When it is a plane , it is called the root surface of the two spheres , and its equation is![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The root plane is perpendicular to the connecting center line of the sum , the center of any sphere in the bundle is on the connecting center line , and the ratio of the sub-connecting center lines is .![]()
![]()
![]()
![]()
[ Spherical sink·root axes of three spheres ] Let the sum be as defined by formula (1) , and let![]()
![]()
![]()
Assume
![]()
where are two independent parameters , then we have![]()
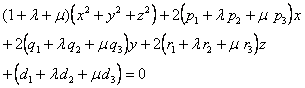
A pair of definite values of the pair represents a spherical surface , and when all values are taken , the whole of the represented spherical surface is called a spherical sink .![]()
![]()
![]()
![]()
![]()
![]()
The root surfaces of each pair of spheres in the three spheres are
![]() and
and![]()
These three planes intersect in a straight line called the root axis .![]()
Second, the ellipsoid
|
Equations and Graphics |
basic elements |
Features |
|
[ ellipsoid ]
When a=b , it is an ellipsoid of revolution ( curve on the Ozx plane It is spherical when a=b=c |
vertex Spindle Principal planes and their equations : Oxy plane z=0 Oyz plane x=0 Ozx plane y=0 The equation of the main axis : AA’ y=z=0 BB’ z=x=0 CC’ x=y=0 Center O (0,0,0) Diameter plane through the center of the plane |
The intersection of any plane and the ellipsoid is an ellipse ( a circle in special cases ). The midpoints of a set of chords parallel to a given direction d lie in a plane , which is a diametrical plane , which is conjugate to the direction d . The three principal planes are diametrical planes that are conjugated to the principal axes respectively . The volume of the ellipsoid : |
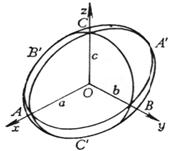
Three, hyperboloid
|
Equations and Graphics |
basic elements |
Features |
|
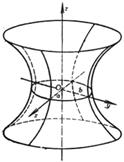
[ Single leaf hyperboloid ]
[ Futaba Hyperboloid ] When a = b , it is [ Rotating Hyperboloid ] ( curve on the Oxz plane obtained by rotating around the z -axis ) |
Spindle Center O (0,0,0) Principal planes and their equations : Oxy plane z = 0 Oyz plane x = 0 Ozx plane y = 0 |
The intersection of a plane parallel to the z -axis with a hyperboloid is a hyperbola ( for a single-lobe hyperboloid , it may be a pair of intersecting lines ). The intersection of a plane parallel to the Oxy plane and a hyperboloid is an ellipse . There are two families of straight generatrixes on a single-leaf hyperboloid , and their equations are ( l is a parameter )
and ( m is a parameter ) |
4. Paraboloid
|
Equations and Graphics |
basic elements |
Features |
|
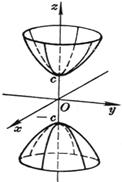
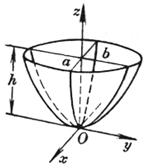
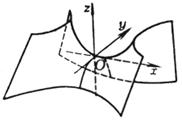
[ ellipse paraboloid ] When a = b , it is a paraboloid of revolution ( The curve on the Ozx plane is obtained by rotating around the z - axis ) [ Hyperbolic Paraboloid ]
|
Vertex O (0,0,0) main axis z axis Principal planes and their equations : Oyz plane x = 0 Ozx plane y = 0 |
The intersection of an elliptic paraboloid with a plane parallel to the z -axis is a parabola ; the intersection with a plane parallel to Oxy is an ellipse . volume
volume
The intersection of a hyperbolic paraboloid with a plane parallel to Oyz ( or a plane parallel to Ozx ) is a parabola ; the intersection with a plane parallel to Oxy is a hyperbola . The shape of the hyperbolic paraboloid is saddle-shaped , so it is also called the saddle surface . There are two families of straight generatrix on the hyperbolic paraboloid , and their equations are and |
5. Cone and Cylinder
|
Equations and Graphics |
basic elements |
Features |
|
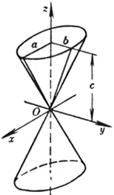
[ Elliptical Cone ] When a = b , it is a conical surface ( The line on the Oxz plane is obtained by rotating around the z axis ) |
main axis z axis vertex origin O a, b are the semi-axes of the intersection ( ellipse ) between the plane of z=c and the cone (ellipse)
|
The intersection of the elliptical cone with the plane z = h parallel to Oxy is an ellipse It intersects the Oxy plane at the origin O.
|
|
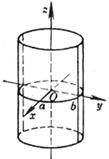
[ elliptical cylinder ] When a = b , it is a cylindrical surface |
The equation of the directrix is The number of directions of the busbar is (0,0,1) |
The intersection of an elliptical cylinder with any plane parallel to Oxy is the same ellipse |
|
[ Hyperbolic Cylinder ]
|
The equation of the directrix is The number of directions of the busbar is (0,0,1)
|
|
|
Equations and Graphics |
basic elements |
Features |
|
[ Parabolic Cylinder ] |
The equation of the directrix is The number of directions of the busbar is (0,0,1) |
|
|
[ Asymptotic Cone ] Secondary cone is a hyperboloid asymptotic cone of |
|
Similar to the asymptote of a hyperbola, the intersection of each plane passing through the z -axis and the hyperboloid is a pair of conjugate hyperbolas , and the intersection with the conical surface is two straight lines , that is, the asymptote of the pair of hyperbolas. . |
6. General quadratic surface
1. General properties of quadric surfaces
For the ellipsoids, hyperboloids, paraboloids, etc. listed above , their equations are quadratic about x , y, and z . The general quadratic equation for x, y, and z is in the form of
![]()
The surface it represents is called a general quadratic surface . Here are some common properties of these surfaces .
[ Intersection point of a straight line and a quadric surface ] A straight line intersects a quadratic surface at two points ( real , imaginary , coincident ). Or the line is all on the surface , at this time it is called the straight generatrix of the quadric surface or busbar .
[ Intersection of plane and quadratic surface ] The intersection of any plane and a quadratic surface is a quadratic curve .
[ Diameter plane and center of quadric surface ] The midpoint of the chord parallel to the known direction of a quadric surface is on a plane , called the diameter plane , which bisects a set of parallel chords . Set the number of directions in the known direction For l , m , n , the equation of the diameter plane is
![]()
or rewritten as
![]()
When l , m , n vary , this equation represents a plane , and the diameter planes of the quadric form a plane . Any plane in the plane passes through the intersection of the following three planes :
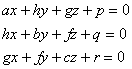
If the intersection point is not on the surface , it is called the center of the quadric surface , and if the intersection point is on the surface , it is called the vertex of the quadric surface . All quadric surfaces with a center are called centered quadrics , and the rest are called quadrics is a centerless quadratic surface .
[ Principal plane and principal axis of quadric surface ] If the diameter plane is perpendicular to the chord bisected by it , it is called the principal plane ( symmetry plane ) . Any two principal planes are perpendicular to each other , and their intersection is the principal axis .
[ Tangent plane and normal of quadric surface ] The equation of the tangent plane of the quadric surface at a point M ( ![]() ) is
) is
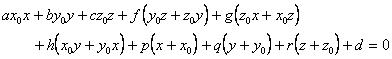
The straight line perpendicular to the tangent plane of the quadratic surface at point M is called the normal of the surface at point M , and its equation can be written as
![]()
[ Circular section of quadric surface ] If the intersection of a plane and a quadric surface is a circle , then the plane is called the circular section of the surface .
If the quadric surface is not a spherical surface , then through a point in space , the quadric surface has six circular sections ; there are generally two real circular sections and four imaginary circular sections ; and several of the six circular sections are coincident .
2. Invariants of quadric surfaces
By the general equation of quadratic surface
![]() (1)
(1)
The coefficients of are composed of the following four functions :
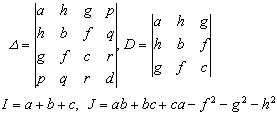
It is called the invariant of quadratic surface , that is, after coordinate transformation , these quantities are invariant . The determinant is called the discriminant of quadratic equation (1) .![]()
3. Standard equations and shapes of quadric surfaces
|
invariant _ |
The equation after coordinate transformation |
Curve shape |
||
|
Concentric Quadratic Surface |
D>0 |
where A , B , C , are characteristic equations
The three characteristic roots of |
A , B , C , when the sign is different, it is a single-leaf hyperboloid A , B , C , no track when the same sign |
|
|
D<0 |
A , B , C , the same sign is an ellipsoid A , B , C , if the sign is different, it is a double-leaf hyperboloid |
|||
|
D=0 |
A , B , C , no track when the same sign A , B , C , when the sign is different, it is a quadratic cone |
|||
|
D = 0 Centerless Quadric |
D<0 |
|
Ellipse Paraboloid ( When both A and B are positive , the negative sign is taken before the square root ; when both A and B are negative , the positive sign is taken before the square ) |
|
|
D>0 |
hyperbolic paraboloid |
|||
|
D=0 |
|
|
When A , B have the same sign, there is no track |
|
|
J = 0 |
|
parabolic cylinder a pair of parallel planes no track A pair of coincident planes |
||
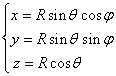
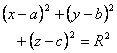
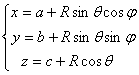
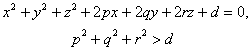
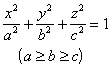

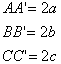
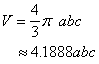

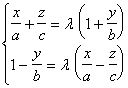
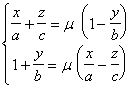
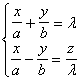 (
( 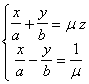 (
(