§ 7  Plane Curve

 

    [ Curve equation and positive direction ]

The form of the curve equation	Forward of the curve
Cartesian coordinate system     Implicit F ( x , y ) = 0      Explicit y = f ( x )  _        parametric or     ( t is an arbitrary parameter , s is the arc length of the curve ) polar coordinate system            r = r ( j )	When x increases , the direction of motion of a point on the curve       When t or s increases , the direction of motion of a point on the curve       When j increases ( that is, counterclockwise ) , the direction of movement of a point on the curve

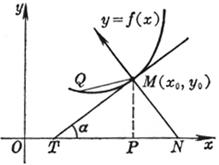
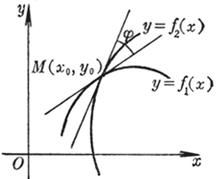
[ The tangent and normal of the curve ] When the point Q on the curve tends to M , the limit position of the secant MQ is called the tangent of the curve at the point M , and the straight line passing through the point M and perpendicular to the tangent is called the normal . The tangent The positive direction of the tangent is the positive direction of the curve at the tangent point, and the positive direction of the normal is the direction obtained by rotating the positive direction of the tangent by 90 ° counterclockwise .

 

    [ Tangent moment, normal moment, secondary tangent moment, secondary normal moment and tangent slope formula of curve ]

	Cartesian coordinate system	polar coordinate system
graphics
Cut distance
normal distance
Secondary distance
subnormal
Tangent slope	tan a

In the table . For the curve expressed by the parameters , in the table

.

   

 

 

 

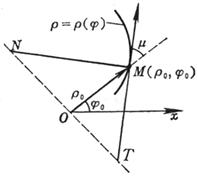
  [ The tangent equation and the normal equation of the curve ]

Curve equation	Tangent Equation ( MT )	Normal Equation ( MN )
F ( x , y ) = 0
y = f ( x )
r = r ( j )

    The table represents the value at the point , same as before .

    [ Included angle of the curve ]  The slopes of the two curves intersecting at the point and the tangent at the intersection point are respectively and , and the included angle j is called the included angle of the two curves ( Figure 7.14), and

          

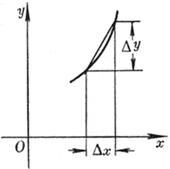
    [ differentiation of arcs ]

Curve Equations and Graphs		Differential of Arc d s
y = f ( x )  r = r ( j )

[ Definition of curvature, radius of curvature, circle of curvature ( or approximation circle ) and center of curvature ]  The ratio between the angle d and the arc length between the positive tangents of two points M and Q on the curve , when Q tends to M , the limit , namely

          

 

It is called the curvature of the curve at point M , that is, the rotation rate of the direction angle of the tangent to the arc length . When k > 0 , it indicates that the curve is concave toward the positive direction of the normal ; when k < 0 , it indicates that the curve is concave toward the normal. Negative direction of the normal ( Fig. 7.15).

                

It is called the curvature radius of the curve at point M. If it is intercepted on the normal line of the concave direction of the curve , C is the curvature center of the curve at point M , and the circle with C as the center and R as the radius is called the curvature of the curve at point M. A circle , also known as a close circle . The coordinates of point C are

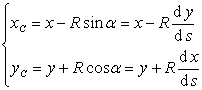
[ Calculation formula of the coordinates of the radius of curvature and the center of curvature ] Let R be the radius of curvature , and ( ) be the coordinates of the center of curvature , then we have

1 ° curve equation is F ( x , y ) = 0

      

When the 2° curve equation is y = f ( x )

     

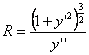
3° curve equation when

                         

                 

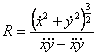
4° curve equation when

                         

             

             

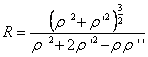
[ Isometric , Involute , Involute and Envelope ]

Definition and Graphics	Equations and Explanations ( G : y = f ( x ))
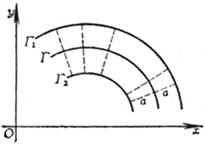
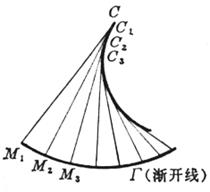
Each point on the equidistant line curve G moves equidistant a in a certain direction ( positive and negative directions ) of the normal of the point to obtain new points , and the trajectory ( sum ) of these points is called the equidistant line of the curve G                    The locus C of the center of curvature of each point on the involute curve G is called the involute of the curve G, also known as the normal envelope of the curve G ( that is, the envelope of the normal of the curve )          The involute curve G is the involute ( or involute ) for its involute C                          Definition and Graphics	In the formula, the upper side of the sign corresponds to , and the lower side corresponds to . This equation is a parametric equation with x as the parameter .   If G is a parametric equation      Then there is an equation with t as parameter         This equation is a parametric equation with x as the parameter . For the equation of the involute of the curve G expressed in other forms, see the formula for the center of curvature               Let the equation of C be y = f ( x ), then G Y = Y ( x ) or      ( x is a parameter ) it is a system of differential equations   The solution of , where      Equations and Explanations ( G : y = f ( x ))
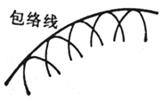
properties of involutes The normal of any point on the   1° involute G is tangent to the curve C   The amount of change in the radius of curvature of two points on the 2° involute is equal to the corresponding arc length of the curve , that is,   The equidistant lines of a 3° involute are the same involutes as it is , they just have different starting points .     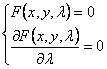A curve whose envelope is tangent to all curves in the family of curves is called the envelope of the family of curves	Involute equations for curves expressed in other forms can be solved by a system of differential equations representing the coordinates of the center of curvature           Implicit ( l is a parameter ) Explicit ( l is a parameter ) Parametric formula ( l is a parameter )   Eliminate l to obtain equations of different forms, and the curves they represent are called discriminant curves , including the envelope and the curve composed of singular points ( for example , the curve family F ( x , y , l ) = 0 points on the trajectories satisfy is a curve composed of singular points ). Therefore, if the curve family F = 0 has no singular point , the discriminant curve is the envelope

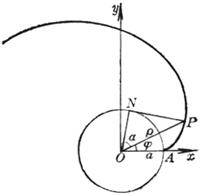
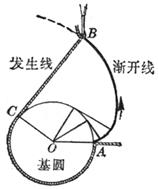
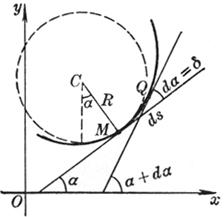
For example , put a thin line that does not stretch around the circumference of the disc , tie a pencil to the end of the line, and pull the end A of the line to gradually open. The curve drawn by the pencil tip on the paper is the involute of the circle . This circle The base circle is called the involute . The thin line is called the occurrence line of the involute ( Figure 7.16( a )). 

Now let's find the equation of the involute . Let the center of the base circle be O and the radius be a . At the beginning of the drawing , the outer end of the occurrence line is at point A , and OA is taken as the x - axis ( polar axis ), as shown in Figure 7.16( b ) .Set the coordinates of the outer end P of the line to be ( x , y ) or ( r , j ), because the original line facing the central angle is a + j ( a = D PON , in gear design , commonly known as the pressure angle ) an arc of Expand into tangent NP , so the length of tangent NP is a ( a + j ), from right triangle ONP : OP = , and because = a + j , thus the involute equation of the circle is obtained

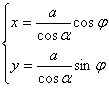
In the formula, a is dependent on the polar angle j , and this relationship is determined by writing the above formula as a polar coordinate equation

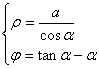   ( a is in radians )

Set t = a + j , the parametric equation of Cartesian coordinates can be obtained

  ( a is the radius of the base circle )

       [ Sherley - Fleiner formula ]

where t and n are the unit vectors of the tangent and normal of the curve, respectively, s is the arc length, and R is the radius of curvature .

       [ Basic Theorem and Natural Equations ]    Given a continuous function k ( s ) on a closed interval [ a , b ] , except for the position difference on the plane, there is a unique plane curve, with s as the arc length, k ( s ) is the curvature . k = k ( s ) is called the natural equation of the curve .

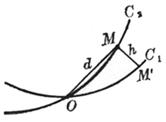
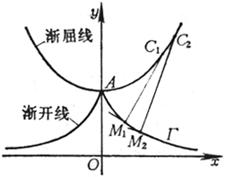
       [ Concepts and conditions of n -order contact between two plane curves ]

       _{Let the two} curves C1 and C2 have _a common point O , take a point M on _C2 , let the _distance from M to C1 be h , and let d denote the distance from M to O (Figure 7.17 ), if

                    

_{Then the two} curves C1 and C2 are said to form nth _- order contact at point O.

       Check the criterion that two plane curves form contact of order n :

       1 ° Let the equation of curve C _{1 be} F ( x , y ) = 0 , and the equation of curve C _{2 to be} x = x ( t ) , y = y ( t ) , and set at point t = t ₀ (that is, O ( x ₀ , y ₀ )) , then the necessary and sufficient conditions for the two curves C ₁ and C ₂ to form n -order contact at point O are:   

where , represents the n -order derivative of j ( t ) .

       The following test criteria can also be derived from this:

       2 ° Assuming that C ₁ : F ( x , y ) = 0 is an algebraic curve (i.e. F ( x , y ) is a polynomial in x and y ), the expansion of C ₂ at the origin (0,0) is   

Then the necessary and sufficient conditions for the formation of first-order contact at the origin are: after substituting the expansion of , the coefficients of , to the power of , are all equal to zero .
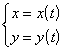
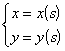
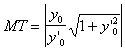
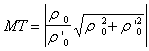
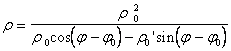
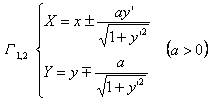
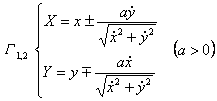