§ 3   Linear Transformation

 

1. Basic Concepts

 

[ Linear transformation ]   Let the sum be two linear spaces on the same field F , and the mappings satisfy the following two conditions:

(i) , for any ;

(ii) , for any ;

Then L is called a linear mapping or a linear transformation, also known as a homomorphism . If and are the same linear space, then L is called a linear transformation of the space V to itself, or an autohomomorphism .

    Example 1 A linear function   on a linear space V (see Section 3) is a linear transformation of V to a field F (considered as a one-dimensional linear space) .

    Example 2   is assumed to be a linear function on a linear space V , then by
                     

The determined mapping is a linear transformation from V to m -dimensional space .

    Example 3   Let V be a real linear space composed of all continuous functions on the interval [ a , b ] . If let

                      

Then L is a linear transformation of V. In fact, because for any real numbers b , c , we have

     

    Example 4   Let V be a linear space composed of all real coefficient polynomials f ( x ) . If let

                  ( the derivative of )

Then L is a linear transformation of V.

    [ Properties of Linear Transformations ]

    1 ^o Conditions (i) , (ii) in the definition of linear transformation are equivalent to: for any

                    

Applying this formula repeatedly, export

                  

    2 If ^o is linearly independent, it is a linear transformation, then

                    

is also linearly independent .

    3 ^o If it constitutes a basis of V , and let , then there is a unique linear transformation L such that .

[ Zero Transformation·Identity Transformation·Inverse Transformation ] The transformation that transforms   any vector α in the linear space V into a zero vector in the linear space is called the zero transformation and denoted as O. That is, for any one , there is

                     ( the zero vector of )

Transforming any vector α in the linear space V into its own transformation is called the identity transformation . Denoted as[Lovely1]  I, that is, for either, there is

                    

Both the zero transformation and the identity transformation are linear transformations .

On the linear transformation L , if there is a linear transformation M on it, such that M is called the inverse transformation of L , denoted as .

[ Matrix of linear transformation ]   Let it be a set of bases of the linear space V , and the base is a linear transformation, then it can be expressed as

             
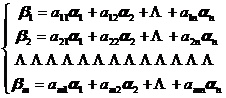
matrix of coefficients

             

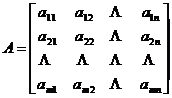
is called a matrix of linear transformation L with respect to bases { } and { } .

In particular, when V is the same dimension as V, or L is a linear transformation of V itself, then A is a square matrix .

After the basis is determined, the linear transformation and its matrix establish a one-to-one correspondence . The matrix of the zero transformation is the zero matrix, and the matrix of the identity transformation is the identity matrix .

    [ Eigenvalues ​​and eigenvectors of linear transformation ] ,   if present , such that the automorphism satisfies

                          

Then the eigenvalues ​​(eigenroots) of the linear transformation L are called eigenvectors corresponding to .

The eigenvalues ​​and eigenvectors of a linear transformation are equal to the eigenvalues ​​and eigenvectors of the transformed matrix, respectively .

[ Rank of image , image source , kernel , linear transformation ] If it is a linear transformation, it is called the image of V, and V is called the image source, and it is called the kernel . The dimension is called the rank of L , and the dimension is called Degeneration times . 

The kernel and image of a linear transformation are linear subspaces of V and V , respectively, and the sum of the dimensions of the kernel and the image is equal to the dimension of the image source . That is

                  

The rank of a linear transformation is equal to the rank of the transformed matrix .

 

Second,  the operation of linear transformation

 

[ Sum and multiplication of linear transformations ] The set of linear transformations   from space V to space , denoted as

                    

is defined according to the following formula :

             

Both new transformations are linear, and

                       

They are called the sum and multiplication of linear transformations, respectively .

By the sum and number multiplication of the linear transformations defined above, the set forms a linear space on F. Its dimension is equal to the product of the dimensions n and m of the sum of V.

    [ The product of linear transformation ] is   set to three linear spaces, if , then define

                    

Obviously a linear transformation from , called the product of linear transformations .

    The product of linear transformations satisfies:

    1 ^o distributive law if then 

                   

    2 ^o Associative law if . 

                       

    [ Idempotent transformation ]   If L is a linear transformation of a linear space V to itself, satisfying the equation

                       

Then L is called an idempotent transformation .

    [ Isomorphism and Automorphism ]   If the linear transformation is one-to-one, then L is called isomorphism, or L is regular . An isomorphism from V to itself is called an automorphism . If the linear transformation of V to itself If the transformation is not an automorphism, it is called a singular linear transformation, otherwise it is called a nonsingular linear transformation (or canonical automorphism) .

    Isomorphism has the following properties:

    The necessary and sufficient conditions for ^1o to be an isomorphism are:

                       

    2 ^o If L and M are isomorphic, , then

                        

In particular, for automorphisms , the above formula also holds .

    3 The set G formed by all the automorphisms of the linear space V on the field F forms a group under multiplication . G is called the linear transformation group of V, denoted by , where n ^is the dimension of V.

    4. The set R formed by all the linear transformations (automorphisms) of the linear space V on the ^o field F forms a ring under addition and multiplication, and R is called the linear transformation ring of A.

 

3.  Dual space and dual mapping

 

    [ Quantity product and dual space ]   Let the sum of V be two real (complex) linear spaces . If a quantity is determined for any pair of vectors , and the following conditions are satisfied:

(i)   

   

(ii) For a fixed and all , if then ; conversely, for a fixed and all , if then . The function is called quantity product .

If , then it is said to be orthogonal . (ii) shows that a vector in one space is orthogonal to all vectors in another space, only if it is a zero vector .

Two linear spaces that define the product of quantities are called dual spaces .

Dual spaces have equal dimensions .

[ Dual basis ]   If the two basis sums of V and V satisfy the relation:

                 

Then they are called dual bases .

    V and V are dual spaces, then for a known base of V , there is exactly one dual base .

[ Orthogonal Complementary Space ]   Let it be a subspace of V, then the set of vectors that are orthogonal to all vectors in space V is a subspace of V , called the orthogonal complementary space, denoted as .

Orthogonal complementary spaces have the following properties:

1 ^o The sum of the dimensions of the space sum is equal to the dimension of the space V , that is
           

^2o _

3 ^o If , then ; and the sum is a pair of dual spaces, and the sum is also a pair of dual spaces .

    [ Conjugate space ]   Let V be a linear space on the field F , if yes , there is a unique number corresponding to F on F , then this correspondence is called a function defined on V.

    function

                           

For any two vectors and any , we have

                  

Then it is called a linear function, also known as a linear functional . Let , then there is , so it is also called a linear homogeneous function or linear type .

    The sum and multiplication of two functions of the set of linear functions in V are defined in the usual way as follows:

           

Then a linear space is formed, called the conjugate space of V , where the zero vector is a function that is always equal to zero .

    It can be shown that and V are a pair of dual spaces, if { } is a set of basis of V , then the function defined by the following equation is a basis of:

                

Thus { } is again the conjugate base of { } .

[ Dual mapping ]   Let V , and W , be two pairs of dual spaces; if two linear mappings:

                 and

For everything and everything , there is

                 

Then L is called a dual mapping .

Dual mappings have the following properties:

1 ^O For a known linear map , there is exactly one dual map .

The rank of the ^2O dual map L sum is equal .

3 ^O A sufficient and necessary condition for a vector to be contained in the image space is that it is orthogonal to all vectors in the kernel .