§ 5   Quadratic and Hermitian types

 

One and  two

 

[ Bilinear ]   If 2 n real (or complex) variables , a quadratic homogeneous polynomial

                                                      ( 1 )

is called bilinear type, where

                   ,

                  

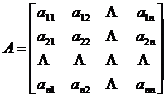
    [ quadratic ]   a quadratic homogeneous polynomial with respect to n real (or complex) variables

                                              ( 2 )

is called the quadratic form, where is the symmetric part of matrix A , that is , the elements of .

The necessary and sufficient conditions for expression ( 2 ) to be always equal to zero are: A is antisymmetric .

When the matrix A is symmetric, the quadratic form is said to be symmetric . When the matrix A is real ( a real number), the quadratic form is said to be real . From ( 2 ), we can see that each quadratic form can be is symmetrical .

A real symmetric quadratic form is said to be positive definite, negative definite, semi-positive definite or semi-negative definite for each set of real numbers that are not all zeros such that , or , respectively . All other real symmetric quadratic forms is called indeterminate (that is , the sign of and is related to) or constant equal to zero .

[ Change the quadratic type to the standard type ]

1 ^o a linear transformation

                                                  ( 3 )

or                       

                    

turn each quadratic ( 2 ) into a quadratic with respect to the new variable

                                                  ( 4 )

in               

or                     

If A is symmetric, then it is also symmetric; if both A and T are real, they are also real .

2 ^o For each real symmetric quadratic form, there is a linear transformation ( 3 ) with real coefficients such that the matrix in ( 4 ) is a diagonal matrix, so

                                                     ( 5 )

In the formula ( 5 ), the number r of the coefficients not equal to zero is independent of the diagonal transformation adopted, and is equal to the rank of the known matrix A, and r is called the rank of the quadratic form . The positive coefficient of the coefficient in the formula ( 5 ) The difference between a number and a negative number is also independent of the transformation applied to the diagonalization (i.e. the Jacobi - Sylvester law of inertia), which is called the sign difference of the quadratic form .

3 ^o In particular, for each real symmetric quadratic form, there is a linear transformation corresponding to the real orthogonal matrix T , which can transform the quadratic form into a standard form, that is,

                                                      ( 6 )

where the real numbers are the eigenvalues ​​of the known matrix A.

4 ^o Perform the transformation again , and the expression ( 6 ) becomes

                    

where is equal to 1 , or 0 , corresponding to the eigenvalue being positive, negative or zero , respectively .

[ Simultaneous simplification of two quadratic forms ]   Given two real symmetric quadratic forms , , which are positive definite, we can find a real transformation ( 3 ), which can simultaneously transform , into the standard form . In particular There exists a real transformation ( 3 ) such that

                

                 

The real numbers are the eigenvalues ​​of matrices , which are algebraic equations of degree n

                     

the root

    [ Method for determining positive definiteness, etc. ] 

    1 ^o The necessary and sufficient conditions for a real symmetric quadratic form to be positive definite, negative definite, semi-positive definite, semi-negative definite, indefinite or always equal to zero are: the eigenvalues ​​of the matrix (which must be real) are both positive and negative, respectively , all non-negative, all non-positive, different signs, or all equal to zero .

           2 ^o A sufficient and necessary condition for a real symmetric quadratic form to be positive definite or semi-positive definite is: every principal subform of

                   

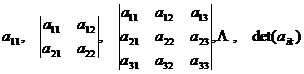
are either positive or non-negative .

3 ^o The necessary and sufficient conditions for a real symmetric quadratic form to be negative definite or semi-negative definite are: positive definite or semi-positive definite, respectively .

4 ^oThe necessary and sufficient conditions for a real matrix A to be positive semi-definite are: . If B is nonsingular, then A is positive definite .

5 ^o If both A and B are positive definite or negative definite, then AB is also positive definite or negative definite . Each positive definite matrix A has a unique pair of square roots Q , .

 

2.  Hermit ( H ) type

 

    [ H -form ]   A quadratic form with respect to n real (or complex) variables

                     

is called a Hermitian type ( H type), where A is an n -order Hermitian matrix (Chapter IV, § 2 , IV), that is .

An H -form is called positive definite, negative definite, semi-positive definite, or semi-negative definite if , for any set of complex numbers that are not all zero , such that , , or , respectively . All other H forms are called indefinite ( i.e. the sign is related to ) or is always equal to zero .

[ Change H type to standard type ]

^1o A linear transformation ( 3 ) turns each H -shape into a new H -shape with respect to the new variable

                 

in the formula                 

or                   

2o ^For each type H , there is a linear transformation ( 3 ) such that

                                              ( 7 )

In formula ( 7 ), the number r of coefficients not equal to zero has nothing to do with the diagonal transformation adopted, and is equal to the rank of the known matrix A , r is called the rank of the H type .

    3 ^o In particular, there is a linear transformation corresponding to the diagonal unitary matrix T for each H type, which can be transformed into a standard type

                                              ( 8 )

where the real arrays are the eigenvalues ​​of the known matrix A.

4 ^o Perform the transformation again , and the expression ( 8 ) becomes

                    

where is equal to 1 , or 0 , corresponding to the eigenvalue being positive, negative or zero , respectively .

[ Simultaneous simplification of two H -forms ] Given two H -forms and , which are positive definite, there exists a transformation ( 3 ) such that 

                 

                 

The real numbers are the eigenvalues ​​of matrices , which are algebraic equations of degree n

                   

's root .

[ Method for determining positive definiteness, etc. ]

    1 ^o A sufficient and necessary condition for an H type to be positive definite, negative definite, semi-positive definite, semi-negative definite, indefinite or always equal to zero is: the eigenvalues ​​of matrix A (which must be real) are respectively positive, all negative, all are non-negative, both are non-positive, have different signs, or are both equal to zero .

    2 ^o A necessary and sufficient condition for a Hermitian matrix A (and the corresponding H -form) to be positive definite or positive semi-definite is that every principal subform of is positive or nonnegative .

    3 ^o The necessary and sufficient conditions for a Hermitian matrix A (and the corresponding H -form) to be negative definite or semi-negative definite are: - A is positive definite or semi-positive definite, respectively .

    4 ^o The necessary and sufficient conditions for a matrix A to be a positive semi-definite Hermitian matrix are: